中国珠算心算协会副秘书长  刘芹英

作为中国珠算申遗的亲历者和见证者，七年前的今天是我最难忘的时刻。在2013年12月4日，当地时间下午五点二十三分，北京时间晚上九点二十三分，在里海之滨、美丽的阿塞拜疆首府巴库，随着联合国教科文组织保护非物质文化遗产政府间委员会第八次会议执行主席一锤落定，全场掌声雷动，“中国珠算”通过评审，正式入选“人类非物质文化遗产代表作名录”。

接着，时任中国珠算心算协会副会长的苏金秀女士代表中珠协作了表态发言：“在保护措施的实施过程中，中国珠算心算协会(CAMAA)将不遗余力地把重点放在发展可行性的策略上，为相关社区、群体或个人施展他们的作用和创造力营造空间。”本人作为中国珠算传承人代表作了表态发言：“我谨代表传承人群体、珠算及珠心算教师和教练师，对委员会决议表示感谢。我们将致力于中国珠算的实践和保护，通过与职业学校、中小学及幼儿园合作，在各教育实验区和实验点传授珠算、珠心算知识和实践技能，发现和培养年轻人才，确保珠算的代际传承。”

申遗成功后，我们在会场外滚动播放中国珠算宣传片，并设置了英文展板供大家阅览；许多国家代表对中国珠算表现出极高的兴趣，特别是非洲国家的一些代表还问，“我们非洲还没有珠算，你们什么时候能传播到非洲来”。

人类非物质文化遗产包括三类：急需保护的非物质文化遗产名录、人类非物质文化遗产代表作名录和优秀实践名册。在2013年，我们的“中国珠算”是中国入选“人类非物质文化遗产代表作名录”的第30个项目。作为我国第一个以知识体系入选的项目，这在当时是一个重大突破。

联合国教科文组织政府间委员会对中国珠算给予高度评价。在决议中指出：“珠算既是中国人文化认同的象征，也是一种实用工具；这种计算技术经世代传承，融入日常生活的多个方面，具有多重社会文化功能，向世界提供了另一种知识体系。将中国珠算列入代表作名录，有利于提升非物质文化遗产的可见度，促进对人类创造力的尊重，尤其是提供了一个适应当代需求的范例。”

联合国教科文组织政府间委员会在对中国珠算的决议英文原文中这样写到“offering the world an alternative knowledge system”中国方面的非遗专家翻译成“为世界提供了另一种知识体系”；也就是说专家将“alternative”翻译成“另一种”，当然这个单词“ alternative”有多种意思。郭世荣教授曾谈到：“英文单词‘alternative’的常规意思为‘二选一’‘另一种选择’，但在没有提供选择成分的情况下，也指‘可替代的’，甚至是‘标新立异’的，《美国传统词典》（英汉双解）解释为：‘Espousingreflecting values that are different from those of the establishment/标新立异的：支持或反映出与正统相异的价值观的’，换言之，‘与传统和主流不一样’。因此，我们是不是可以把‘offering the world an alternative knowledge system’译成‘（中国珠算）向世界提供了一种颇具特色的知识体系’？此处翻译成‘颇具特色’比‘另一种’更能反映珠算在世界计算技术史上的地位和意义，也符合原文的语境。相信这也是非遗委员会的专家们对中国珠算的认识。”以上是郭世荣教授的意见。

下面我谈一下自己对翻译的看法。说到将“alternative”翻译成“另一种”时，我们当时也跟中国社会科学院巴莫曲布嫫教授探讨过，最后还是没有改动。个人观点认为不管是将“ alternative”翻译成“另一种”还是“二选一”、“标新立异”“与传统和主流不一样”、“颇具特色”等等，都说明中国珠算有自己独立的知识体系，而且是与其他知识体系不同的。

对于中国珠算知识体系的研究，是一个大的研究课题，需要数学界、数学史界、数学教育界和珠算界专家学者携起手来、下大力气来共同研究知识体系及其科学性。

鉴于此，再加上对珠算界对珠算文化特性研究和探索相对较多，如抓周礼仪、婚嫁、邮票、绘画艺术、文化作品、戏曲和歌曲，还有建筑等方面都涉及到珠算文化，也是大家有目共睹的。相对而言，学界对珠算科学性的研究相对较少。今天在这里谈谈自己对中国珠算科学性的认识。不当之处，还望各位同仁多提宝贵意见。

对照现代计算机来看，中国珠算的硬件是算盘、软件是口诀和算理算法等。下面从硬件和软件两大方面来阐述中国珠算的科学性。

一、中国珠算硬件的科学性

说到算盘，历史上还有其它国家也有算盘，除中国算盘外，比较著名的还有：罗马算盘、俄罗斯算盘和欧洲划线算板等。只不过其它国家的算盘大多已被淘汰。

（一）以珠作为“算子”的科学性

1.算珠数量的界定

显然，只用一颗珠子作计算是不够的。但是用很多珠子，来作计算，既繁又慢，也是不可取的。用几个珠子作加减，形象，直观，拼拆即可。

如：+=，-=；既形象表达了加减的含义，又极易完成加减的运算(拼拆珠子而已)，运算过程与结果，可以直观出来。

+，即便珠子不太多，操作也甚麻烦，而且不能一下子直观出来加数与得数来。说明珠子多了不易运用累积的思想方法计算。用多少珠子累积比较合适呢？我们的祖先凭借经验，5个以下的珠子容易直观出来。

中国祖先的智慧与近代心理学家耶文斯（W.S.Jevens）的实验结论不谋而合。近代心理学家耶文斯（W.S.Jevens）1871年曾经做过“黑豆实验”：在黑色背景前随机抛下黑豆，下面用白色盘子接住，当落到盘中的豆粒一停下，就让受试者立即说出盘中黑豆数。他共做了1027次，实验结果是：凡是黑豆粒在5颗以内，准确率为100％；当豆粒为5颗，准确率只有95％；黑豆粒数愈多，报对的次数占的百分比愈小；当豆粒达到10颗时，报对的次数只有43％。“黑豆实验”说明人的视觉直观累积个数的极限是4。因此，用算珠示数计算，累积的珠数不宜超过4。

从上面汉代徐岳所著的《数术记遗》中对“珠算”的描述及甄鸾的注释来看，说明了两点：一是中国古人已经掌握了人视觉直观累积个数的规律；二是要表示超过4的数或更大的数，可以借助空间位置。

在这一点上，俄罗斯算盘就显得笨拙一些。（如下图）：

实际上，我国现在小学生现在使用的计数器（如下图）就是俄罗斯算盘的一种变形。

2.珠形设计及承载方式

中国算盘是有梁串档设计，珠型是椭圆型、菱形、还有蝶形等，我们看罗马算盘珠的形状是圆形的，为了防止滑动，要设计成沟槽算盘（如下图）：

看似差别不太大，实际上，“基因”处的微小差别，对后续影响是非常大的，不能说“差之毫厘，谬以千里”吧，也差不多。

珠作为算子，不仅要能静能动，还要达到“静而稳，动而速”。但是，动起来之后要停在哪里？怎么让它停下来？就需要有个恰当的控制办法，否则，就难以做到准确、迅速。中国古人摸索确定的办法，就是在需要停止的地方用横木挡住，这样，用手拨动算珠时，可以放心大胆地拨，不必考虑何时停、怎样停的问题，到停的地方被横木挡住就会自然停下。这样一来，不仅使操作算珠至为简易，还保证了拨珠的高速度。

3.示数的直观性

中国算盘设计时，只用累珠数与空间位这两个“要（因）素”，不仅解决了0—9十个基数的表示问题，同时也保证了示数的直观性。

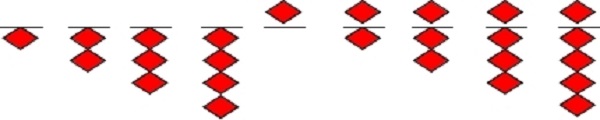
基数1—9 在中国算盘上的示数方法

我们现在感觉这种设计并不难，好像很容易想到和做到。事实上，历史上并非各地域、各民族祖先都会这么做，都能做得这样恰当。例如，西方人的祖先就是采取如下的方法组织算珠的。

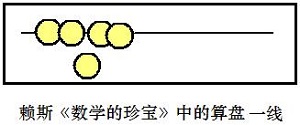
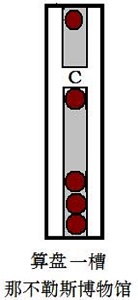
在表示一位数时，可能大家随示数直观性的感觉并不是很显著，表示多位数时差别更明显：如在算盘上表示五位数28,041。

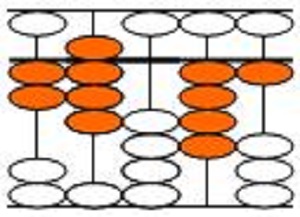
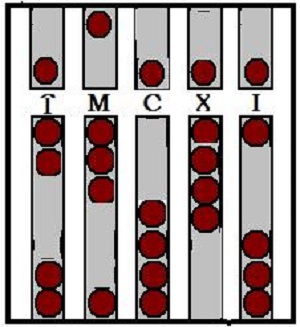
（二）中国算盘“设梁”的科学性

1.体现了五升十进制

中国古人在算盘上用梁区分一档的上、下位置，从而使累数、位值思想方法都能充分发挥作用，不仅形象，而且直观。同时，还保证了在示数、进行运算时的准确性和高速度。十进位值制的10个基数，都能用算珠表达出来了，不仅形象，而且直观：

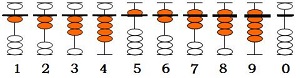
用算珠表达的基数，可称为珠码。显然每个珠码都能直观出来——即一眼就能看出来，根本察觉不出分辨它们所用的时间。

2.运用空间周期思想

容易看出：算盘的一档就是一个周期。多个档无非就是一档的重复。因为运用位值思想方法，这个空间位置不同当然非常重要，一般用“位数”（…，6，5，4，3，2，1，•, 0，－1，－2，－3，－4，－5，…）来区别（其中 • 称为小数点）。为便于掌握各档位数，可在梁上设点——如每3档设一点，运用时可指定某一点做小数点，从而各档的位数就确定了。

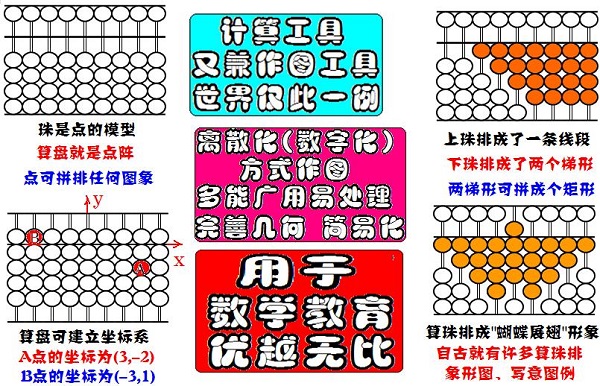
3.兼具图具功能

中国算盘上的算珠还可以看做珠阵图，具有现代电子计算机点阵图的部分功能，可以作为电子几何点阵作图即数字化作图工具。如果将其用于数学教育非常适合儿童，不仅可以填补了点阵几何的空白，还能简化和完善几何教学。

二、中国珠算软件的科学性  

主要从以下六个方面谈中国珠算软件的科学性。

1.珠码符号有计算功能

古代珠算的四则运算均采用口诀，加减法口诀、乘法口诀和归除口诀。珠算口诀的特点是，既精炼又押韵，又郎朗上口，不仅便于诵读，而且便于记忆和操作。

现代珠算已经不再采用口诀，而是采用通用数学法则。加减法已经符号化了，只需26个动珠码，拼排珠码符号即可完成计算；乘法采用空盘前乘法；除法采用商除法，只需要九九口诀即可。周所周知，乘法要转化为加法，除法要转化为减法。而且珠码符号容易内化，有利于心算能力的形成。

利用算盘构造出了既简捷又有计算功能的符号——珠码符号，只需把表示数的珠码符号拼排在一起即可完成数的运算。例如计算6+2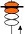，拼在一起就是。

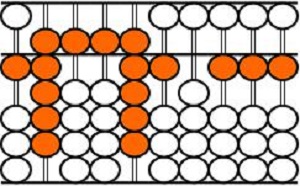
由于珠码符号具有计算功能，只需用26个动珠码（如下图）符号就可以完成加减运算。

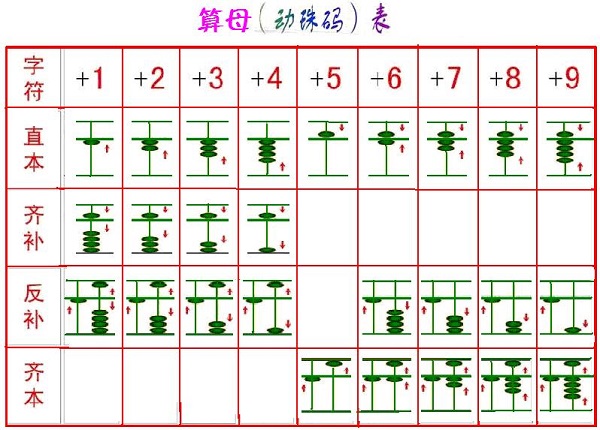
这里借用上海珠协张德和老会长的一个观点：笔算和筹算都是“概念计算”，需要借助人的口算或心算，而珠算符号本身就有计算功能。

2.珠算运算模型与计算机一致

中国珠算虽然古老，但其运算模型与现代计算机是一致的，而笔算运输模型与计算机不一致，甚至可以说是矛盾的。例如：325+654-753=226

3.珠算可以“二元示数”

珠算的二元示数概念是相对于笔算的一元示数而言的。历史上，每个国家都有一套自己的记数法，但并不是所有国家的记数方法都可以二元示数。中国算盘不仅靠梁算珠可以示数，靠框的算珠也可以示数，而且在上一下四珠的算盘上，梁珠数与框珠数是互为补数关系。

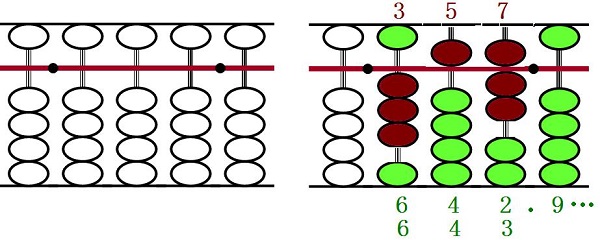
二元示数不仅大大简化正负数认识及运算，如代数运算，使得大数减小数与小数减大数运算顺一致，不需要颠来倒去；还能简化珠算乘法和除法运算。

4.珠算算法是通用算法

珠算法程序式，省储存空间，是世界上唯一普适于手操算、脑算、电子计算机的通用算法模型；适合于手操作算、脑算和计算机算。

例如：计算325+654-753=226

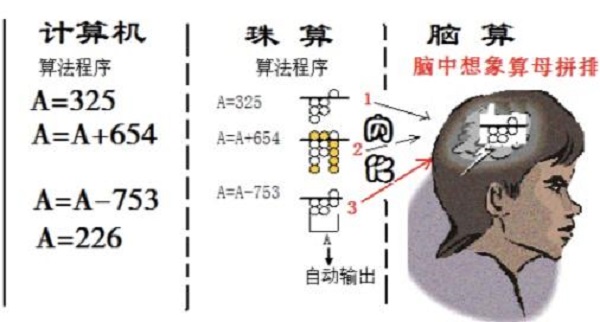
5.珠算算法的一体性

珠算机制能够集输入、储存、施算、输出一体完成，直观快速无比，使计算直观易形成直觉。

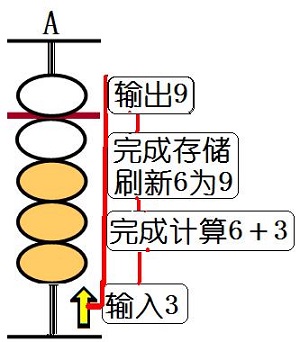
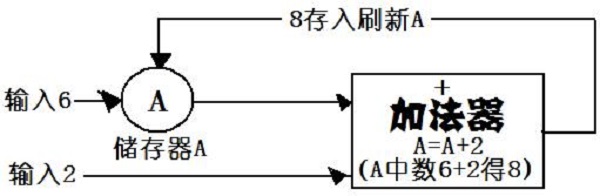
6.珠算数形（结合）一体

珠算数形一体，亦数亦形，算具兼图具，尤其对于数学启蒙教育具有独特优越的意义。

以上，我从硬件和软件两个方面了解了中国珠算所具有的科学性。也正是因为中国珠算具备这样的科学性，才能在历史的长河中经久不衰，延续下来并不断创新发展。

三、中国珠算的创新发展

在珠算基础上创新发展起来的珠心算，不仅具有强大的计算功能，更是对开发儿童智力潜能具有显著作用。将珠算珠心算应用于数学启蒙和基础教育，充分发挥其教育功能和开智功能。

下面举三个例子来说明珠算珠心算对数学启蒙和基础教育的简化作用。

1.二元示数对四则运算的简化作用

二元示数大大简化了正负数的及其运算。如下题：

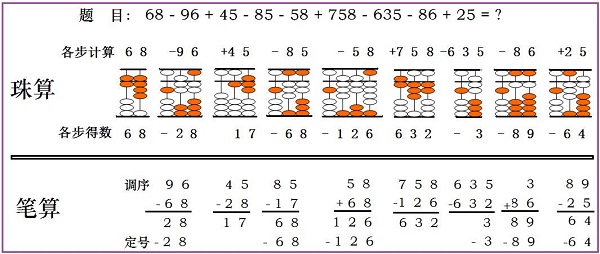
以乘法为例：99999×9999，左下图是明代王文素给出的算法；如感觉题中靠梁珠数大，计算繁难。可用它的框珠数，框珠数小（两个因数中的一个用框珠数即可），计算很简捷。

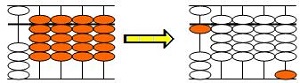
二元示数对于除法的简化，就是创新了“代数除法”和“二元除法”，时间关系，这里不再详细介绍。

2.珠阵图对几何进行的简化作用

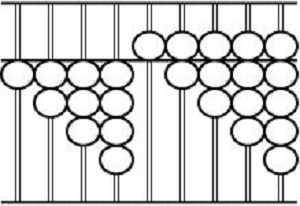
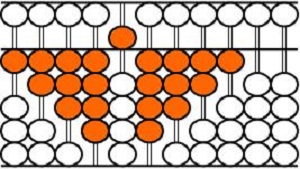
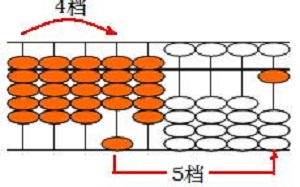
珠图是离散方式表达的图形，容易识别、操作、处理。如下图中算盘图下珠组成的珠梯形，如果用一个算珠作面积单位，那么，使用数数的方法也可求出其珠面积（如左白珠梯形珠面积是14珠，红色珠梯形的珠面积是28珠）；用它推导梯形的求面积公式，也很容易，这些工作幼儿园的孩子都能够完成。

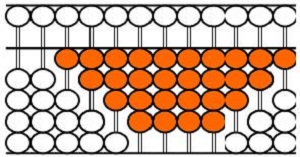
总之，离散的图形方式把几何简易化，体现“理-象-数”思想方法，可以实施几何的早教育。

3.分数运算

鉴于时间关系，这里只举一个分数减法运算的例子，对于分数的约分和加法运算同样适用。

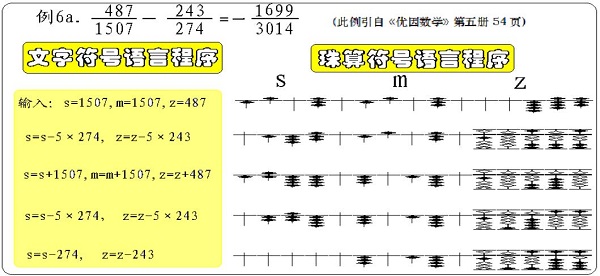
从图中可以看出，最后得到的分数是最简分数，也就是说约分和减法运算是同时完成的。而且该题目也运用到了“二元示数”。

由于时间关系，仅举以上三个例子来说明珠算珠心算对数学启蒙和基础教育的简化作用。实际上，用珠算不仅对现行数学教育有非常大的简化作用，而且完全可以进行数学教学，还可以构建新的数学教学知识结构。珠算界的前辈郭启庶教授早在2002年就开始了“优因数学”教学实验工作。经过18年的教学实验，达到了预期效果。即三年就可以完成原本六年的教学任务，大大减少了教学时间。

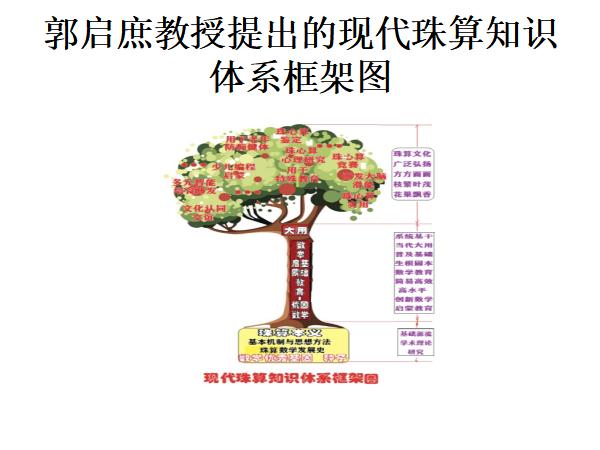
上面是郭启庶教授提出的现代珠算知识体系框架图，如果按照郭启庶教授提出的现代珠算知识体系框架图，我今天所讲的内容仅是根部的一小部分。所以说，对于整个珠算体系的研究，还需要我们大家的共同努力。

谢谢大家！