
中国珠算心算协会副会长、内蒙古师范大学科学技术史研究院二级教授 郭世荣
摘要:使用算器进行计算是中国传统数学的一大特色,算筹和算盘作为计算工具在古代数学中发挥着极为重要的作用。研究筹算与珠算在传统算法设计中的作用,对于更加深入地理解中国数学的算法设计思想及算法特点的形成颇有帮助。本文将包括以下几方面的内容:第一,概要说明筹算与珠算的基本规则与操作规程的主要特点;第二,分析若干筹算算法设计的案例;第三,在案例分析的基础上总结筹算算法设计的主要思想;第四,讨论珠算在筹算算法设计基础上对算法的进一步改进与发展;第五,研究筹算与珠算对于中国传统数学特点形成的作用与意义。
关键词:筹算、珠算、算法设计
中国古代使用算筹和算盘进行计算,形成了完整且独特的筹算和珠算使用规则与操作程序,自成体系。对于中国的筹算、珠算及中国传统数学的特点等,学界已有很多探讨,成果不胜枚举,例如李俨对中国筹算的研究,华印椿等对珠算的研究,吴文俊对中国传统数学的机械化、构造性和算法化特征的论述,都早已为学界所熟知。算筹和算盘这两种计算工具对于中国传统数学特点的形成发挥了极为重要的作用。算具与算法二者相互依存,相互配合,相互影响,从而形成中国传统算法的特色。而算法设计很好地反映了中国传统数学的推理论证和思维模式,更影响了数学文本编写。以往对于中国传统数学特点的形成与算具间的关系讨论较少,这是本文将要讨论的主要问题。
1.筹算与珠算的规则与操作
使用算具进行计算是中国古代数学的一大特色[1]。为了阐明计算工具与算法之间的关系,有必要先扼要说明筹算与珠算的运算与操作。
我国很早就建立了一套筹算演算制度[2],形成了筹算体系,包括算筹的规格与形制、用算筹纪数的方式、运筹方式、计算规则、算法设计、记录方式,等等。约在宋代,我国开始有了用笔写筹式进行计算的方法[3],明代中后期筹算基本上被珠算完全取代,明末《同文算指》等著作传入了西方笔算,但筹式符号(包括暗字码)作为数学记录符号一直被使用到清末。而朝鲜和日本的数学家直到18世纪仍然以筹算为主要计算工具。

筹算的纪数基础为“十进制”和“位置制”,用算筹将数字按高位在左、低位在右的方式摆在筹算盘(算案)[4][5]上。为了防止相邻数位上的算筹相混,规定了“一纵十横,百立千僵,千十相望,万百相当”的摆筹方式,即每一个数字有纵横两种筹式,在实际使用时,一个数的相邻两位数字以纵横筹式区分。算筹摆放的位置很重要,在不同位置上的算筹表示不同单位上的数字。用筹无法表示数字零,就空开一位。为了减少用筹和简洁,又采用“五升制”,即:1~5用累积筹表示, 6~9用一根置于上方的筹表示5,其余部分在下方仍用累积表示(图1),上方代表5的筹和下方代表1的筹也纵横不同,此即《孙子算经》所言:“满六以上,五在上方。六不积算,五不单张。”古代还用赤黑二色筹或以筹的“邪正”来区分正负数,例如刘徽在注《九章算术》方程章时就讲到“正算赤,负算黑,否则以邪正为异。”在宋代的书写记录中则采用在数字的最后一个筹式符号上打一斜杠表示负数。
在实际计算中,计算加法时将被加数摆在算板上,从数的高位开始逐位加上加数,当一个数位上满十时就向前一位进位。计算减法也是从减数的高位开始逐位从被减数中减去。即加减运算在一横行中进行。计算乘法时,先将实(被乘数)和法(乘数)分别置于上下二行,再将法数向左移使其末位数与实数的首位数对齐,然后用法的每一位数分别乘实首位数,并遵循“言十即过,不满自如”的规则按位将积(乘得的结果)置于中行,并将积数按数位随时相加。当全部法数都与实首位乘完后,移去实首,法退一位,再与实第二位相乘,并将积与前积相加。继续这个步骤直到实每一位都被乘完(“上下相乘,至尽则已”)。这是我国自古就采用的筹算乘法,但相关的记载较晚,在《孙子算经》中才有明确记叙。后来还有尾乘法,即从实的末位乘起。计算除法时,“凡除之法,与乘正异。乘得在中央,除得在上方。”兹不细述,详见《孙子算经》。因此,乘除法需要是在三行中完成的。唐代后期,有将乘法简为二行者,甚至简至一行。开方计算则根据开方次幂的高低在多行中运算。
概括地讲,筹算有以下特点:
第一,筹算通过在筹算板上摆放算筹来实现运算,根据运算需要,算筹被摆放在一行或多行上。
第二,算筹在筹算板上摆放的相对位置很重要,不同的位置代表不同的数学意义,例如分数的整数部分及分子与分母、方程组中的不同方程及方程各未知数的系数等都是由算筹摆放的位置表示的。同时,位置也与运算过程和操作直接相关。
第三,用筹计算时,不保留中间过程,每位数字运算完即把旧数字改为新数字。
珠算是以筹算为基础发展起来的,是筹算体系的进一步扩展与发展,珠算借鉴和发展了筹算的许多东西,同时也反过来扩充和丰富了筹算体系,使筹算运算表现出了更加灵活多样的特点。至明代后期珠算体系完全形成,包括算盘的结构形制、算盘中数的表示、算盘的拨珠方式和用指方法、珠算的口诀、书写表示、算法设计、运算技术与技巧,等等。
设计算盘时采用了筹算的“五升十进”思想。算盘中以梁上一珠表示5,梁下一珠表示1,并用档位决定数位,这继承了筹算表示数字的思想。同时,算盘在梁上设计了二珠,这样一个档位上最大可表示15,后来又发展出悬珠的用法,使一个档位上可表示更大的数,这是珠算在筹算基础上的创新。宋代杨辉在筹算表示中也采用在一个筹式的上方增加代表五的筹的方法在一个数位表示大于9的数①,这或许是受到珠算影响的结果。
珠算计算加减法也是一次完成,即先在算盘中拨入被加数或被减数,然后从高位开始按数位逐位加减,直到运算结束。这与筹算加减法在本质上无区别。在计算乘除法时,先在算盘上拨入法、实(明代规定法右实左),然后以实为主进行计算。乘法以法的每一位乘以实的某一位,头乘法从实首位开始,尾乘法从实末位开始,依次相乘,乘得的结果随时相加,实的任一位数乘讫即变,所谓“实动法不动”。除法则只能从高位除起,但是也有归除、商除等不同的演算方式,与筹算所不同的是直接把实变成积或商。乘除法相当于筹算的一行算法。开方则相当于把筹算的自上而下的纵向多行排列搬到算盘上横向排列。
筹算与珠算除了算具不同外,在算法和操作方面既有联系又有区别。在操作方面筹算主要是摆筹及其规则,珠算则是拨珠、指法、口诀应用,等等,二者的所遵循的数学原理基本相同。在算法上,珠算继承了筹算的几乎所有算法,同时也发展出了一批适合在算盘上运算的新算法和改进算法。其实筹算算法也在不断改进和创新中。例如,宋代杨辉与元代朱世杰等人就给出了不少新算法,这些算法同时适应筹算和珠算,一方面反映了珠算早期发展的过程,另一方面也反映珠算对丰富筹算的作用,二者交互影响。
筹算与珠算既有共同的地方也有其各自的独立特点。筹算和珠算都需要通过对算具的操作来实现运算,这决定了与其相应的计算必须是可以通过操作算筹或算盘来实现,并在有限步骤内可以获得结果;用算筹摆放数和用算盘表示数都采用十进制,都对位置有严格的要求;在运算中都使用口诀,但珠算口诀更重要;在记录和图示方面,珠算继承和借用了筹算的书写表示法,特别是筹式符号,记录基本上没有太大的改变,但是增加了算盘图。二者也有一些不同点:当需要多行运算时,筹算按上下纵向行展开,珠算则只能在一行内完成,如果非得多行不可,珠算只能把多行平列在一横行中(例如开方);珠算拨珠有指法要求,从而提高运算速度,筹算则对运筹速度无要求(虽然古人有赞扬某人运筹如飞的情况),因此,珠算有加快运算速度的要求,筹算则没有;筹算将摆筹的位置与算法紧密结合,有的算法设计充分考虑了摆筹的空间与位置的作用,而珠算则在这方面可发挥的空间较小;珠算有一些只适合于算盘上实现的特殊算法。
计算工具必须与算法相结合才能实现其运算功能,筹算和珠算演算共同要求算法要具有可操作性,即用计算工具(算筹或算盘)可实现,因此古代算法一般都包括计算的过程和演算的次第,并依此设计了相关的算法程序。中国古代数学的构造性特点与此关系极大。算筹和算盘对算法和计算过程有不同的要求,对算法设计有很大的影响。中国早期的算法与筹算紧密结合,体现筹算特点与特色,宋元以后又出现了不少适合珠算的算法。这些算法共同构成中国古代数学的核心部分,体现了中国数学与其它文明数学的不同特征与特点。
2.筹算算法设计案例
中国早期数学著作中的算法是通过算题体现出来的,算题包括“题”“答”“术”,后来又增加了“草”或“细草”。其中术最为重要,术即是算法,给出解题方法。不过,并不是每题都包括术和草,有时一术统御多题,适应于解决一类问题,可称之为通术。同时也有些题的术只给出本题的具体演算,是通术的具体化,这里暂时不考虑这些术。
古代数学家一般很少说明算法是怎么设计出来的,但是通过分析算法的构造和它们所强调的重点内容可以看出其设计思路和思想。为了在下一节中阐明算法设计的思想,作为案例,这里先分析《九章算术》方田章的“平分术”和少广章的“少广术”。
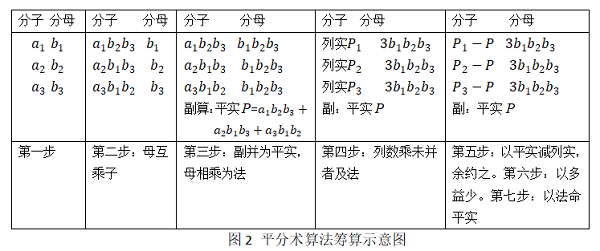
例1 平分术
“平分术曰:母互乘子,副并为平实,母相乘为法。以列数乘未并者,各自为列实。亦以列数乘法。以平实减列实,余约之,为所减。并所减,以益于少。以法命平实,各得其平。”

其筹算运算过程的示意图如图2。
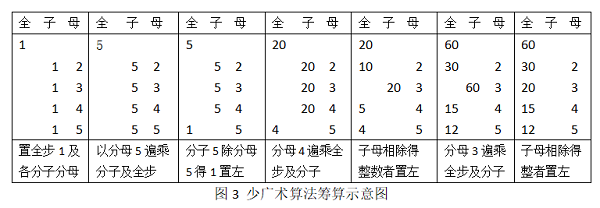
例2 少广术
“少广术曰:置全步及分母子,以最下分母遍乘诸分子及全步,各以其母除其子,置之于左。命通分者,又以分母遍乘诸分子及已通者,皆通而同之,并之为法。置所求步数,以全步积分乘之为实,实如法而一,得从步。”

兹以n=5为例,列出此术所给出的运算过程如图3:

3.以筹算操作为中心的算法设计思想
平分术与少广术的设计反映了中国古代数学算法设计一个重要思想,即以筹算的操作为中心进行算法设计。其主要思想和设计重点如下:
第一,算法设计围绕筹算演算过程展开
算法的设计以筹算的操作为中心,体现筹算的演算过程,形成筹算运算程序。以上述二例言之,如果以数学原理为中心设计算法,平分术应该说明把要平分的几个分数相加再除以分数的个数得平均数,然后求出平均数与各分数之差,再以所多的部分补所少的部分。少广术则只需说明以一亩积步240步除以各分数之和即可。但是《九章算术》没有采用这样的术文,而是把重点放在了通分的演算过程上。平分术给出了用算筹计算的过程,先将各分数通分为同分母分数,再置各分子相加,算出各分数相和后的平均数的分子,然后算出各分数分子与平均数分子之差,接着“以多益少”使各分数均等,最后通过除法运算给出平均数。少广术也是完全依据筹算的操作为中心设计的。此术所要解决的是一个分母为若干分数相加的除法问题,最终目标是算出这个除法的法和实,而算法设计的重点是各分数的通分过程。因此,这些算法的设计都以筹算运算过程为中心,指导读者通过筹算演算来解决问题。算法所给出的内容,重点在如何操作筹进行演算。
第二,算法设计包括筹算板的空间利用
算筹在筹算板上摆放的位置是算法设计要考虑的重点因素之一。筹摆放的位置具有重要的数学意义。这表现在几个方面:
首先,利用筹的位置来表达这些筹所代表的数学意义。如上述二例中的分子、分母、及整数部分的位置不能错,乘除法运算中的法、实、积或商的位置都是固定的;线性方程组表示中不同的位置代表不同未知数的系数或常数;天元式与四元式的每一个位置都被赋于了不同的数学意义,不同位置代表方程的不同次幂的系数。
其次,在设计算法程序时,同时考虑利用好位置来实现运算,如开平方、开立方和开高次方的算法都充分发挥了位置因素的作用。
再次,用与位置相关的术语和语汇来指导操作,如前二术中提到的“副置”“最下分母”“置左”等。筹的位置关系极为重要,是算法设计中一个必须进行设计的部分。算法设计充分利用位置关系来实现算法程序的可操作性和简洁性,体现算法的程序性。如盈不足术:“置所出率,盈、不足各居其下,令维乘所出率,并以为实。并盈、不足为法。副置所出率,以少减多,余,以除法、实,实为物价,法为人数。”不仅明确指示了“所出率”“盈”及“不足”的位置关系,而且使“维乘”的意义十分清晰。
第三,算法设计指明筹算的操作过程
在算法中包括操作过程的设计,对每一步操作都有明确的指示,上述二例都包括这样的指令。在其它算法中也可以看到大量这样的操作指令,如开方中的“借算”“步之”“超(若干)等”“折法而下”“方一、廉二、下三退”,还有“副置”“副并”,等等。通过操作来实现算法目标,指明操作过程,把操作过程作为算法的不可或缺的组成部分,这是算法设计的重要内容。
第四,算法设计重视用筹复杂度
使用筹的多少和运算复杂度问题是古代算法设计所考虑的因素之一,古代数学家认为用筹少的算法是好算法。刘徽在注《九章算术》方程章最后一题时就指出要考虑用筹多寡,他批评“拙于精理”者不会变通,不考虑使用算筹的复杂度问题:“其拙于精理徒按本术者,或用算而布毡,方好烦而喜误,曾不知其非,反欲以多为贵。故其算也,莫不闇于设通而专于一端。至于此类,苟务其成,然或失之,不可谓要约。”他主张要像庖丁解牛那样灵活掌握算法:“夫数,犹刃也,易简用之则动中庖丁之理。”他“记其施用之例,著策之数”,计数了“方程新术”和“其一术”用筹的数量[6]:“如此凡用七十七算”“如此凡用一百二十四算也”,以用筹多少来说明其方法的简易性,强调“凡九章为大事③,按法皆不尽一百算也。虽布算不多,然足以算多。”在方程章第一题的注文中也强调要避免用算筹繁而不省:“即计数矣,用算繁而不省。所以别为法,约也。”李淳风注算经十书强调“凡为术之意,约省为善”,《夏侯阳算经》也说:“夫算之法,约省为善。”例如,对于少广术,李淳风就说明“亦不宜用合分术,列数尤多,若用乘则数至繁,故别制此术,从省约。”指出了这样设计少广术就是为了避免运算繁复。
中国古代数学中在上述思想指导下设计的算法很多,仅以《九章算术》而言,与通分约分相关的约分术、合分术、减分术、课分术、平分术、大广田术、少广术、衰分术等都是以筹算操作为中心设计的。这些算法都与处理不同分母的分数有关,是古代数学的重点和难点,而通分是关键。刘徽将通分(他称之为齐同术)视为“算之纲纪”,他在注合分术时写道:“然则齐同之术要矣。……乘以散之,约以聚之,齐同以通之,此其算之纲纪乎!”《张邱建算经》开首即言:“夫算学不患乘除之为难,而患通分之为难。是以序列诸分之本原,宣明约通之要法。”《夏侯阳算经》也强调:“凡除分者,全数易了,奇残难用,心意之劳,正在于此。”这应该是算法设计把操作作为重点的前提。
此外,《九章算术》中的开方术、开立方术、盈不足术、方程术等术以及宋元时代发展起来的各种开高次方、大衍术、天元术、四元术、垛积术、招差术等等算法的设计重点也都在说明演算过程。这些算法都要求有极精细的筹算操作过程,所以设计的重点都在如何通过操作来实现最终的演算结果。
以筹算操作为中心设计出来的算法当然是以数理原理为基础的,不过这些算法本身很少讲原理,而是把算理寓于算法之中④。这并不代表古代算法都是在这种思想指导下设计的。中国古代以数学原理为中心进行算法设计是算法设计的另一大类型,这类算法重点讲述数学原理,而较少关注演算过程。仍以《九章算术》为例,求各种田形面积和各种立体的体积的算法,与分数相关的经分与乘分,与除法相关的其率术与反其率术、今有术及返衰分术,由开方术导出的开圆术和开立圆术以及勾股术等等算法,都是以数学原理为中心的思想指导下设计的。例如,刘徽就十分注重解释说明算法的数学原理,他的《九章算术》注的核心就在于为算法补充说明数学原理,李淳风注也是如此。这样,以筹算操作为中心和以数学原理为中心两种算法设计思想形成的互补,共同铸就了中国传统算法的特色。李继闵曾以“率”概念为中心梳理《九章算术》中的算法,将许多算法统归于率的演化与发展这个纲纪之下[7],阐明这些算法互相间的逻辑递进关系。他也十分强调算器在中国传统数学中的重要地位:“中国传统数学自始至终都与算器的应用密不可分。虽然世界各个民族的数学发展史上都使用不同的算器,但是很少有像中算这样对算器的明显依赖性,以致可以用‘筹算’二字来代表中四古代数学。”[8]
4.珠算对算法设计的影响
明代中后期,珠算取代筹算成为传统数学的主要计算工具,但是在珠算取代筹算之前有很长的筹算与珠算并行期。珠算不仅继承了大多数筹算算法,而且也改进和创新了不少新的算法。
在宋元时代的数学著作中可以看到筹算与珠算相互影响的影子,宋元时期大量新算法的出现应是筹算与珠算相结合的结果。大约成书于五代时期[9]的《谢察微算经》已涉及珠算术语和内容,珠算在宋代已有相当的流传。南宋数学家杨辉继承了唐代以来寻求便捷算法的思想[10]。他追求算法的多样性和简捷性,积极探讨各种便捷的乘除算法或其替代算法,强化了一些旧有算法,同时也利用归、因、损、折、倍、求一等方法对乘除数和被乘除数进行处理,设计了一批新的算法,使身外加法、身外减法、定身除等等算法流行起来。其基本思想是:“制算之法,出自乘除,法首从一者,则为加为减。题式无一者,则乃折乃倍。以上加名九归,以下损名下乘。盖副乘除,羽翼算家之妙。”[11] 强调“伸引变通”和灵活应用。他还设计了各种代乘、代除算法,根据不同的数字灵活选择最便捷的算法。从北宋初的“增乘法”到南宋杨辉时代的“九归新括”、归除、飞归、穿归,再到元代朱世杰《算学启蒙》中的撞归法、起一法,宋元时代给出了除法的一系列新算法[12]。在乘法方面发展出破头乘、掉尾乘、留头乘、隔位乘、身前乘、身后乘等等不同的算法,这些算法都是同时适合筹算和珠算的。口诀也在宋元数学著作中逐渐流行了起来。以往认为,这些都是筹算对珠算的影响,实际上,它们既是筹算算法自身发展的结果,也是筹算与珠算相互影响的结果。当时的数学著作延续了以筹算语言撰写文本的传统,所以给后人形成了它们都是筹算算法的印象。
珠算继承了很多筹算算法,有不少算法被直接搬到算盘中运算,如各种各样的乘除法,有的则被改造成合适在算盘上运算,如将乘除法的法、实以及开方术的商、实廉、隅等数从都从原来的纵向排列改成在算盘上横向排列,将原来的三行或二行算法简化为一行算法,等等。珠算也使原来筹算中不太流行的方法变得更加流行和普及,如归除法、撞归法、飞归法、先十法等,发展了一批独特的算法,出现了各种“杂法”,如“二字奇诀”“金蝉脱壳”“众九相乘”以及悬珠的使用等。珠算与心算结合紧密,为后来珠心算迅速发展奠定了基础。珠算家们编制了大量的新口诀,不仅方便流传与普及,而且促使诗词歌诀在数学著作中广为流行,元代后期以后,可以说无诀歌不成算书。
珠算算法设计的基本思想是适合在算盘上操作完成,强调操作的方便性与简捷性,如“金蝉脱壳”,是乘除法的原始形态,但是其大流行则主要是因为在算盘上运算的原理十分简洁,操作时可以不加思考地进行运算。再如,明代很多著作中都有“定位”相关的内容,这是专门为珠算设计的。
5.筹算、珠算与中国传统数学的特色
计算工具在算法设计中起了很大的作用,因此对中国数学特点的形成也发挥了很大的作用,对数学推理与数学思维以及数学文本的形成也有重要的影响。
计算工具在中国古代数学中所发挥的作用是其它数学文明无可比拟的。以筹算为中心的算法设计要求算法必须是可操作的,即在有限步内可完成,因此必须是构造性的和机械化的。在筹算算法设计中,数学家充分认识到可重复实施的算法结构的重要性,充分发挥其作用,使循环结构大显身手。从《九章算术》到清代从未间断过对这种算法结构的应用[13]。以明安图为代表的清代数学家接触到西方无穷级数时,他们首先想到的就是用递归循环结构来表达无穷级数,使之成为研究无穷级数不可或缺的重要工具,对清代中后期的数学研究颇有影响。循环结构是机械化和构造性算法的重要特征之一,对中国传统算法特点的形成发挥了重要作用。
筹算操作方法在古代数学推理与数学思维中也大有作为。算法本身就与数学推理与数学思维的结果。以筹算操作为中心进行算法设计,其实质就是从筹算操作的角度进行思维和推理,把算理和演算操作紧密结合在一起,而最终以操作的形式表述思维和推理的结果,这就形成了中国数学寓理于算的特点。有些推理与思维过程表面上似乎与筹算的联系不是很紧密,但是细究起来都离不开筹算的操作。古代的算术的思维与推理本身就是从筹算出发的,而代数的运算与推理也同样建基于筹算,其中有些推理又与几何相结合,这样就形成了筹算与几何相结合来解释代数的思想,演段术是这种思想的重要体现。三国时代的数学家刘徽与赵爽对许多算法的解释,以宋元时代的数学家们对其方法的解释都包含着筹算的操作的内容。
古代数学文本的撰写也尽量使用筹算的语言,从算题到推理都以筹算操作为重点,形成了数学文本的风格。数学文本的核心部分为“术”和“草”,术给出算法,而草就是筹算演算过程。在具体算题中,很多术文出同样是直接给出演算过程。这里举《孙子算经》中二例。
今有兽六首四足,禽四首二足,上有七十六首,下有四十六足,问禽兽各几何。
答曰:八兽七禽。
术曰:倍足以减首,余半之,即兽。以四乘兽,减足,余半之,即禽。
此题术文只给出如何操作方法,而其原理是寓于计算过程之中的:“倍足”后,禽之首足数相同,而兽则首比足多二,所以“倍足以减首”所余为兽之倍,故半之得兽数。“四乘兽”数为兽之共足数,“减足”所余为禽足数,禽二足,故半之为禽数。
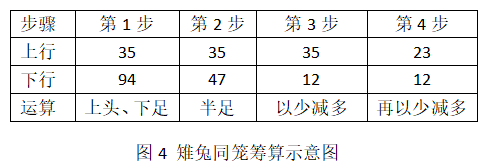
今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何。
答曰:雉二十三,兔一十二。
术曰:上置三十五头,下置九十四足,半其足得四十七。以少减多,再命之。上三除下三,上五除下五。下有一除上一,下有二除上二⑤,即得。
又术曰:上置头,下置足。半其足,以头除足,以足除头,即得。
此题也是只给操作过程,并且给出摆放筹的上下位置(图4)和运算的口诀,而将算理隐于计算过程中。从算理上看,下位足数半之,所余为一倍雉数和二倍兔数,当然多于“上”位总头数。执行“以少减多”,即从下位减去上位总头数,下位所余为一倍兔数。“再命之”,即再“以少减多”,即上位总数头数减去下位兔数,所余为雉数。
古代算经十书中这样的行文方式随处可见,比比皆是。这种以筹算为中心的文本书写方式是中国传统数学著作书写的重要风格。
总之,筹算与珠算对于中国传统算法设计中发挥发重要作用,具有重要意义,是研究中国数学特点的形成、数学文本的风格和数学推理等都必须考虑的内容,值得深入研究。同时,也必须指出,算具和算法是相辅相成的,是一对孪生兄弟。它们是共同成长,一起发展的,很难说哪个为主,哪个为辅。前面我们重点讨论了一个侧面,即筹算和珠算对算法设计的意义,我们不应忽视另一个侧面,即算法如何塑造了筹算。
【参考文献】
[1]中外数学简史编写组. 中国数学史[M],山东教育出版社,1987,10-11.
[2]李俨. 筹算制度考[A],中算史论丛(第四辑),科学出版社,1955,1-8.
[3]李迪. 宋元时期数学形式的转变[A],中国科学技术史论文集(一),内蒙古人民出版社,1991,219-233.
[4]严敦杰. 筹算算盘论[J],东方杂志,41:5(1945),33-34.
[5]李兆华. 关于算筹和筹算的几点注记[A],陕西师大学报,1987年第1期。收入李兆华《古算今论》,天津科学技术出版社,2000,128-135.
[6]魏雪刚、郭世荣.《九章算术》方程章“麻麦”问刘徽注中“算”字新释及方程“旧术”新校[J],自然科学史研究, 35:1 (2016),2016,10-17.
[7]李继闵. 《九章算术》与刘徽的比率理论[A],吴文俊主编.《九章算术》与刘徽,北京师范大学出版社.,1982,228-245.
[8]李继闵. 《九章算术》导读与译注[M],陕西科学技术出版社,1998,35-36.
[9]李迪、冯立升. 《谢察微算经》试探[A],李迪主编. 数学史研究文集,第三辑,1992,58-65.
[10]梅荣照. 唐中期到元末的实用算术[A],钱宝琮主编. 宋元数学史论文集,科学出版社,1966,10-35.
[11]杨辉. 乘除通变算宝(序)[A],郭书春主编. 中国科学技术典籍通汇·数学卷一,河南教育出版社,1993,1047.
[12]李培业. 中国珠算简史[M],中国财政经济出版社,2007,53-59.
[13]斯日古冷、郭世荣. 《九章算术》及其刘徽注中几个算法的循环结构分析[J],内蒙古师大学报(自然科学版),2012年第3期,321-324.
【注释】

作者简介:郭世荣(1959-),内蒙古师范大学科学技术史研究院二级教授,国际科学史研究院通讯院士,主要研究方向数学史、中外科技交流史、少数民族科技史。担任国际数学史委员会执行委员(2015-)、中国科技史学会副理事长(2018-)、中国珠算心算协会副会长(2018-),曾任中国数学史学会数学史分会理事长、中国科技史学会数学史专业委员会主任和少数民族科技史专业委员会主任。






