第一部分: 研究报告综述
“珠心算对认知功能的影响及其神经机制的研究”项目研究报告
浙大、中国科大联合实验组
1.研究背景
1.1 关于珠心算研究的国内外背景
珠算(Abacus calculation)是中国的传统文化之一, 珠心算(Abacus mental calculation)是传统的珠算和心算结合的产物,长期的珠心算练习使练习者形成了独特的、以“珠像(Abacus imagery)”为媒介的数字感知和计算方式,即把抽象的数字变成直观的算珠影像,并在头脑中“打算盘”。与普通心算相比,珠心算练习者运用特殊的运算法则,形成了特殊的数字结构和提取、加工信息的方式。他们不仅有更快更强的心算能力,还具有更强的数字记忆能力。珠心算“手、眼、脑”协调操作的特点及其练习产生的效果,引起了儿童教育界人士的关注,同时也引起了心理学家和认知神经科学家的兴趣。一些研究者通过具体的教学实践认为,珠心算练习不仅对提高儿童的计算能力有促进作用,而且对其他方面的大脑功能和认知品质的发展也有促进作用。也有学者担心珠心算练习通过形象思维促进儿童数学计算能力的发展,可能会影响儿童数学抽象推理能力及其他的认知能力的发展。目前,还没有一个合理的科学证据来解释这两个方面的观点,而在全国一些地区的幼儿园和小学开展着珠算/珠心算的教学。针对这种情况,有必要开展科学实验研究,考察珠心算练习对儿童认知能力的影响及其神经机制,为儿童珠心算教学实践提供理论指导。
当前,脑和心智的研究是具有重大科学意义的战略性科学领域,2007年9月10位美国著名科学家曾在《Science》上撰文建议设立“心智十年”(a Decade of the Mind Initiative)计划。揭示脑与行为的关系是当前生命科学领域中面临的重大挑战之一,数字认知是人类数学能力的基础,数学抽象推理是人类逻辑思维的核心。珠心算是一种特殊的心算技能,对珠心算的神经机制的研究是一个重要的科学问题。国内外众多研究人员对此进行了不懈的探索研究。日本科学家Hatano是用实验手段研究珠心算的心理机制的先驱,他发现珠心算专家比普通人有更强的数字记忆广度,他推测珠心算专家在数字工作记忆时可能更多地采用了视觉空间表征的策略,在脑中形成了珠像。芝加哥大学学者Stigler 通过实验证实11岁的中国儿童经过珠心算练习有更强的心算技能。著名学者Miller 发现长期的珠心算训练会影响成人对数量的空间表征。由于实验手段的限制,这些早期的实验都是行为测量,虽然对珠心算的心理机制提出了可能的解释,但是没有脑机制上的进一步的证据。随着脑功能成像技术的发展,日本学者Hanakawa和Tanaka等人分别用功能磁共振技术对珠心算的神经机制和数字工作记忆的神经基础进行了初步的探索。
总的来说,国内外对珠心算的研究还很初步,基本上处在行为学的经验观察和描述阶段,对珠心算神经机制的研究甚少。因此,研究珠心算练习对认知功能的影响,探索珠心算的神经机制显得尤为必要。
立项过程
针对珠心算国内外的研究现状,浙江大学物理系交叉学科实验室自2003年起就开始对珠心算的神经机制进行初步的探索。2005年,在财政部、教育部的支持下,受中国珠算心算协会委托,浙江大学物理系交叉学科实验室和中国科技大学神经生物学系成立浙大、中国科大联合实验组承担“珠心算对认知功能的影响及其神经机制的研究”项目。
2.研究项目介绍
2.1 研究目的
考察珠心算对认知功能的影响及其神经机制。
2.2 研究内容
借助于先进的实验仪器,深入了解珠心算练习对大脑功能的影响及其机制,主要进行以下几个方面的研究:1、珠心算的神经基础及其脑区的活动机制;2、珠心算对脑区功能连接的影响及其机制;3、珠心算练习对注意、工作记忆、空间认知加工的影响及其机制。
2.3 研究方法
本项目发挥多学科交叉优势,从心理学、认知神经科学、医学、计算机科学、物理学等不同层面来共同探究珠心算练习对认知功能的影响及其心理机制和神经机制,在方法手段上利用心理学行为测量、事件相关电位技术和磁共振成像技术等现代脑成像技术,从行为、功能、结构三个不同水平、不同角度考察问题。
3. 研究结果
3.1 珠心算练习对儿童数字认知加工的影响
3.1.1 珠心算练习对儿童心算的神经机制的影响
实验目的:利用功能磁共振成像技术考察珠心算的神经机制
实验结果与结论:在本研究中,珠心算儿童和普通儿童分别完成简单的一位数连续加法和复杂的连续加法。通过功能磁共振成像技术,我们发现,这两组儿童在做心算的时候,参与的脑区是有差异的。在进行心算加工时,珠心算儿童的左侧语言区没有明显的激活,而在两侧颞叶后部或顶上小叶后部有显著的激活,这个现象表明珠心算加工不依赖于语言表征,而更多地依赖于视觉空间表征。而普通儿童在心算时,左侧语言区域有显著的激活,这与前人的研究结果相吻合,该现象进一步证实在心算过程中,普通儿童采用了语言相关的策略。本研究表明珠心算的神经机制可能有别于普通心算,主要依赖视觉空间表征,本研究可能为因语言区受损而导致的计算缺失的病人提示了康复治疗的途径。
3.1.2 珠心算练习对儿童精算和估算的影响
实验目的:结合事件相关电位技术和功能磁共振成像技术考察珠心算练习是否会影响儿童精算和估算的脑机制。
实验结果和结论:功能磁共振实验表明,珠心算儿童在精算和估算任务下,脑区的激活没有显著的差异;而普通儿童在两种任务下,有较大的差异,特别是在估算任务下有更多的脑区参与活动。事件相关电位实验表明,珠心算儿童在脑电的波形和幅值上没有显著差异(400ms之间),普通儿童在完成精算和估算任务时,额叶和顶叶区域脑电的幅值有显著的差异。实验结果表明,长期的珠心算练习,可能会促进儿童的数学计算能力,珠心算儿童在精算和估算任务中可能采取非语言依赖的视觉空间策略。对普通儿童来说,采用的计算策略不是单一的,在精算任务中,可能主要依赖语言策略,在估算任务中,语言表征和非语言的视觉空间表征可能都有参与。
3.1.3 珠心算练习对儿童数字数量自动加工的影响
实验目的:用数字Stroop范式来考察珠心算练习是否能促进儿童对符号数字数量的自动加工。在实验中我们考察了两组被试在两种任务下(数值比较和形状比较)的顺应效应和距离效应,同时也比较了干扰效应、易化效应,以及两组儿童在形状比较和数值比较时的加工速度的差异。
实验结果和结论:形状比较任务下的顺应效应和距离效应是检测是否对数量信息进行自动加工的重要标志,而干扰效应(干扰率)和易化效应(易化率)是检测数字自动加工程度的一个有效指标。在形状比较任务中,珠心算儿童在反应时上有显著的顺应效应和距离效应,而普通儿童只有顺应效应,这个结果说明珠心算儿童和普通儿童都能对符号数字的数量信息进行自动加工,但这不足以反映这两组儿童对数字自动加工的程度是否有差异,所以我们进一步对干扰和异化效应进行组间比较,分析结果表明在形状比较任务中,珠心算儿童比普通儿童有更大的干扰效应,这说明珠心算儿童比普通儿童对数字数量的自动化加工程度更深,然而,在本实验中,珠心算儿童和普通儿童在易化效应上并没有发现显著的组间差异。
3.1.4珠心算练习对儿童数量空间表征的影响
实验目的:通过检测珠心算儿童和普通儿童在数字/符号表征的数量比较及奇偶判断任务的SNARC效应和距离效应来考察珠心算练习对儿童数量空间表征的影响。
实验结果和结论:珠心算儿童只有在数字数量比较任务中表现出SNARC效应,而普通儿童在数字数量比较任务和数字奇偶判断任务中均未表现出SNARC效应;珠心算儿童在符号-数字数量比较任务中表现出了SNARC效应,而普通儿童在这项任务中却没有;珠心算儿童的距离效应比普通儿童更接近于成年人的模式。以上实验结果表明,珠心算练习可能促进了儿童数量与空间表征的联结,加速了抽象数字认知的发展。此外,两组儿童在圆点比较任务中都表现出SNARC效应和距离效应,而且没有检测出显著的组间差异,这个结果意味着珠心算练习对数量的符号表征影响较大,而对数量的非符号表征影响较小。
3.2 珠心算练习对其他认知功能的影响
3.2.1 珠心算练习对儿童工作记忆广度的影响
实验目的:考察珠心算练习对儿童数字和字母的工作记忆广度的影响。
实验结果和结论:分析表明,珠心算儿童在短时数字记忆广度上显著高于普通儿童,珠心算练习者在字母记忆广度方面也显著高于普通儿童。以前的研究表明珠心算练习能提高数字记忆广度,而我们的结果显示珠心算练习者在字母记忆广度方面也显著优于普通儿童,我们推测珠心算可能扩大了个体的工作记忆容量,因此对于数字以外的对象也有较高的记忆广度。如果这一推断成立,那么珠心算练习就对个体的发展具有积极而深刻的影响,因为工作记忆容量对个体的认知能力以及注意能力等都有非常重要的作用。
3.2.2 珠心算练习对儿童执行注意的影响
实验目的:结合注意网络行为实验和脑电技术来考察珠心算练习对儿童执行注意的影响。
实验结果和结论:实验发现在声音提示-目标反应这样一个反应注意网络的实验中,一般儿童在提示与目标间隔时间为400毫秒时执行注意水平比没有提示的情况下差,而珠心算儿童却没有这样的差异。这个结果表明珠心算儿童在注意资源分配能力方面优于一般儿童,因此当存在注意资源竞争的时候,他们的执行注意水平并不会受到显著的影响。而我们在3.2.1中提到珠心算儿童的工作记忆广度显著高于普通儿童,且已有研究表明工作记忆广度长的个体比短的个体有更高的执行注意水平,而且能够更加灵活分配注意的资源,因此本实验中所发现的注意水平的组间差异可能与珠心算练习对工作记忆的影响密切相关。另外,脑电实验的结果表明两组儿童在典型的脑电成分(P300,N2,及LPC)在某些脑区有显著的差异,这些差异进一步支持了行为的结论:即珠心算儿童可能在注意资源分配能力上优于普通儿童。
3.2.3 珠心算练习对儿童表象能力的影响
实验目的:考察珠心算练习对儿童心理旋转能力的影响
实验结果和结论:本实验采用字母F和抽象图像作为刺激材料,发现珠心算儿童完成心理旋转任务的准确率显著高于普通儿童,反应时间也明显低于普通儿童。在补充实验中也发现,两组儿童在简单任务(看到刺激出现就按键反应)中无显著的组间差异。本实验表明,珠心算练习可能能够促进儿童表象操作能力的发展。
3.3 珠心算练习对脑结构的影响
实验目的:利用弥散张量成像技术来考察珠心算练习对儿童脑白质的影响。
实验结果和结论:结合实验3.2.1,经分析表明,珠心算儿童在短时数字记忆广度上显著高于普通儿童,个体的短时数字记忆广度与其脑结构存在相关关系;我们发现珠心算儿童在与视空信息处理相关的脑区如前运动区的神经通路、枕-颞联合区及胼胝体前部和中前部显示出较高各向异性分数,这个结果表明珠心算练习可能能提高儿童的工作记忆容量,同时能加强视空信息处理相关的神经通路的发展。
此外,神经结构方面的发现为理解珠心算的神经机制提供了重要的线索,也为训练在脑发育过程中产生的影响提供新的证据。我们推测珠心算儿童在某些脑区结构有别于普通组的原因主要有两个:1)珠算过程中左手的频繁使用,2)在珠心算的过程中,珠心算儿童可能调用了更多的视觉空间信息处理的神经资源。
4. 小结
本项目自立项至结题的3年多时间,课题组共在4个省份7个城市、测试600余人次、实施35个实验(22个行为实验、 5个脑电实验、 8个fMRI实验)。参加实验的珠心算儿童主要由小学二、四、五年级学生组成,有1-4年的珠心算学习经历,期间每周约练习2-4小时。
通过一系列实验,得到以下主要实验结果:
一、珠心算的神经机制与普通的心算有差别,珠心算加工过程更多地依赖双侧前运动区和顶叶后部等与视觉空间加工相关的脑区,而普通心算加工过程更多地依赖左侧语言脑区,珠心算练习有可能在一定程度上提高儿童在视觉空间信息加工方面的能力。这个实验结果也为因语言区受损而导致的计算缺失病人提示了康复治疗的途径。
二、珠心算儿童与普通儿童在大脑的白质一致性(white matter integrity)上存在一定的差异,主要表现为珠心算儿童在胼胝体后部和中前部、右侧前运动区投射和左侧枕颞联合区这些神经结构上比普通儿童具有更高的白质一致性,这个结果意味着珠心算练习可能促进了视觉空间信息相关的神经通路的发展,这个结果也是珠心算练习可能影响到儿童其他认知能力(如表象操作)的神经基础。
三、珠心算儿童与普通儿童在精算和估算的神经机制、数量的自动加工和空间表征方面存在一定的差异。珠心算练习可能提高儿童在精算和估算任务中的效率、减少需要的资源;珠心算练习可能提高儿童对符号表征数量的自动化加工程度,可能促进儿童数量-空间联结的发展。
四、珠心算儿童与普通儿童在工作记忆方面存在差异。珠心算儿童不仅在数字记忆广度上显著 高于普通儿童,而且在字母记忆广度方面也显著高于普通儿童。由此,我们推断珠心算练习可能扩大了个体的工作记忆容量,对于数字以外的对象也有较高的记忆广度。如果这一推断成立,那么珠心算练习就对个体的发展具有积极而深刻的影响,因为工作记忆容量对个体的认知能力以及注意能力等都有非常重要的作用。
五、珠心算儿童与普通儿童在注意和心理表象操作方面存在不同程度的差异。珠心算练习可能提高儿童分配注意资源的灵活性,提高儿童的表象操作能力。
珠心算是一种特殊的心算方式,是传统的珠算和心算结合的产物。本项目在方法上利用心理学行为测量、脑电和磁共振等现代脑成像技术,并发挥多学科交叉优势,从心理学、认知神经科学、物理学等不同层面来共同探究珠心算练习对儿童认知功能的影响及其神经机制,从行为水平、脑功能和结构多个层次对珠心算练习对儿童的数字认知、其他认知功能及脑结构的影响及其神经机制等进行了初步的探索。
5. 致谢
项目执行期间得到了浙江大学以及中国科技大学有关领导和老师的支持;财政部和中国珠算心算协会为项目的实施提供了很多物质支持和便利;各参与测试的学校和相关医院在实验过程中与我们真诚合作;特向他们表示真诚的感谢!
我们特别要感谢参与实验的全体儿童和他们的家长,没有他们的参与,就没有本项目的成果。
再次对以下单位表示衷心的感谢:中国珠算心算协会、黑龙江珠协、浙江省珠协、山东潍坊市珠协、慈溪市珠协;七台河第一小学、潍坊北关小学、慈溪第三实验小学、杭州九堡镇九堡小学、杭州康桥小学、解放军军事经济学院及上海市普陀区的小学等;浙江大学第二附属医院、上海同济大学附属同济医院、哈尔滨医科大学附属第二医院、青岛大学附属医院等。
第二部分: 研究成果汇报
2.1珠心算练习对儿童数字数量自动加工的影响
陈飞燕
1、引言
数概念与空间和时间概念一样,都是人类抽象思维的基本要素。而个体对数量信息的表征是获得数概念以及发展更高级的数学能力的基础。在数概念中,数字的意义将随着语境的不同而不同,Fuson[1]认为与数相关的语境主要有三类:数的语境(基数性),序列顺序语境(序数性),与数无关的语境(非数字性)。在此基础上,Wiese[2]进一步指出,数字在这三种语境中分别代表了数量、数序和非数字意义。在基数性的语境中,数字表达了“多少”的意义,即数的量;在序数性的语境中,数字表示在序列中的相对位置,如“第几”的意义;非数字意义是指将数字当作标签,如几号。这可以用一个例子来说明,如“尽管34号球员跑出了78码的成绩,但是熊队由于失去两次触地得分的机会,排名滑落到第六位”(Despite a seventy-eight yard run by number thirty-four the Bears lost by two touchdownsdroppedsixth place)[3],该例子中分别体现了数字在三种不同语境中的意义。而在所有的数字意义当中,数量的意义一般被认为是最重要的,数量信息的加工也是人类日常最重要的思维活动之一。人们不仅能准确地把握具体事物的数量,而且能对抽象符号所代表的数量信息进行操作和加工。
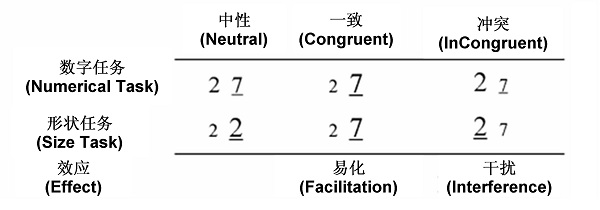
比较两个数字的数值大小(5>3)是人类最基本的数学能力。如果要求被试对一个数字与另一个给定的数字之间的大小进行判断,或要求对两个任意数字之间的大小进行判断,通常会发现随着两个数字之间的距离减小,判断的难度增加,这就是所谓的数字距离效应[4]。另有研究发现,数字的尺寸形状大小也会影响数字大小判断;数值的大小也会影响形状的判断[10]。如同时呈现的两个数字,让被试判断这两个数字的数值大小或者形状大小,结果发现,数值和形状之间会相互影响,在形状比较时,数量信息会被自动激活;同样,在数值比较时,形状的信息也会被自动激活。这就是数值-形状干扰效应(number–size interference effect), 这种实验范式被称为数字Stroop任务(Numerical Stroop Task),是经典的颜色-单词 Stroop 任务的变式。在数字Stroop任务中,形状判断时,在顺应条件下比在中性条件或者冲突条件下,被试的反应要快得多,也准确得多,如判断以下三对数字的形状大小:3 8,3 8, 3 8,前者要比后两者快得多,这也就是所谓的顺应效应(congruity effects)。数字Stroop范式,常常用来考察是否存在数字自动加工。判断数值大小要求被试对数字刺激本身的数量信息进行加工才能做出反应,其加工程度较深;判断数字的形状大小(即当前任务是非数字加工任务),需要抑制数值大小无关的信息,其对数字进行较浅的加工。顺应效应被认为反映了在加工形状维度信息时抑制数值自动加工的难度。形状比较,是一个知觉维度的任务,相对来说发展的更早;符号数字的数值比较是教育的结果,相对成熟的较晚;对数值比较而言,形状比较存在加工优势。从某种意义上来说,数值维度加工的速度和准确率反映了数字加工自动化的发展变化过程:数值比较的准确率越高速度越快,说明数字加工自动化的程度越高。因此在形状比较任务中的距离效应和顺应效应,被认为是考察是否存在数字数量信息自动加工的两个重要指标。
符号数字加工自动化是教育的结果[5,6],与学习、教育密切相关。但迄今为止,对数字加工自动化的研究大多是从发展的角度来考察的[5,6],几乎没有研究探讨教育、训练对儿童数字加工自动化的影响,对技能训练的研究,大多集中在考察训练对工作记忆、智力等方面的影响[7,8]。而珠心算是一种特殊的心算方式,珠心算练习为考察儿童数字加工提供了很好的途径。最近的研究表明,手指训练能够提高年幼儿童的数学能力,有研究认为手指的灵活程度和数学能力有密切的关系[9]。值得一提的是,珠心算操作需要双手协同工作,对手指的灵活程度要求非常高。而且,儿童往往在6岁左右开始学习珠心算,这个年龄段对儿童数学能力的培养非常重要。由此,我们推断长期的珠心算练习可能能够促进儿童对符号数字数量信息的自动化加工。
在本研究中,我们采用数字Stroop范式,珠心算儿童和对照组儿童需完成两个任务,判断两个阿拉伯数字的数值大小同时忽略形状的大小,或者判断两个阿拉伯数字的形状大小忽略数值大小。
本研究的主要目的是考察珠心算组儿童和对照组儿童对数字自动加工的程度的差异。我们预期得到以下结果:一、因为参加本实验的儿童的年龄已经足够大,足以形成对数字自动加工的能力,所以珠心算组和对照组在形状判断任务时,都存在顺应效应和距离效应。二、本实验中也包含了儿童数量加工能力与执行功能中抑制能力的关系,基于之前的假设,我们预期得到这样的结果:在不一致的情况下,进行形状任务,由于珠心算组对数量的激活越来越趋于自动化,这种自动加工的趋势难以抑制,使干扰效应增大。而在数值比较任务中,珠心算组的干扰效应相对应对照组要小。三、在对照组中,形状信息加工占绝对的优势,总是得到优先加工;而在珠心算组中,这种优势被明显削弱,数值信息的激活越来越趋于自动化。本研究中,顺应效应和干扰效应的大小将作为衡量数字自动化加工程度的指标[5,6]。
2、研究方法
实验对象:本研究包括30名年龄在9-11岁的身体健康珠心算儿童(男17人,女13人,平均年龄= 10.20 ± 0.535岁)和30名同样年龄段身体健康的普通儿童(15 男,15女,平均年龄 = 10.08 ± 0.543 岁)。这两组儿童来自同一个学校、同一个年级的不同班级,接受相同的常规的小学教育,唯一不同的是珠心算组儿童每周接受3-4小时的珠心算练习,持续约3年时间。对照组没有进行珠心算练习。两组儿童都进行了中国儿童韦氏智力测试(WISC-R),对照组平均 IQ = 109.87±6.19; 珠心算组平均 IQ = 107.34±8.62。
刺激和方法:实验任务分为两类,即判断两个阿拉伯数字的数值的大小或者数字的形状大小。我们设置了大小两种距离(数字之间距离为1:2-3、7-8,距离5:2-7、3-8)和三种不同条件(一致:数值大而且数字的形状也大,如 2 7;不一致:数值大但形状小,如 2 7;中性:在数值判断时,形状大小一样(如 2 7),和形状大小判断时,数值大小一样(如2 2)。数字的形状大小分别为40号、45号、50号的Arial字体。刺激为黑底白字,呈现在17寸的纯平显示器中间,分辨率800×600,刷新频率为75赫兹,实验时被试的眼睛与屏幕中心的距离约为60cm,注视点与被试眼位处同一高度。刺激由E-Prime呈现。
实验设计与程序:实验采用2(组别:珠心算组和对照组))×2(任务类型:数值判断和形状判断))×3(刺激类型:一致性、冲突和中性))×2(距离大小:距离为1和5)。首先呈现500ms的注视点,然后注视点消失,在注视点的两侧出现两个数字,要求被试又快又准确的按左右键(F,J)选择准确答案,在被试做出反应或延时2000ms后,开始下一次试验。试验开始前,每位被试均要求完成72次练习,正式实验中,一半被试先做数值判断任务,另一半先完成形状判断任务。实验分为四组,组间休息至少45秒,被试如果需要可以延长休息时间。每种任务下的实验刺激随机呈现。
3、结果与分析
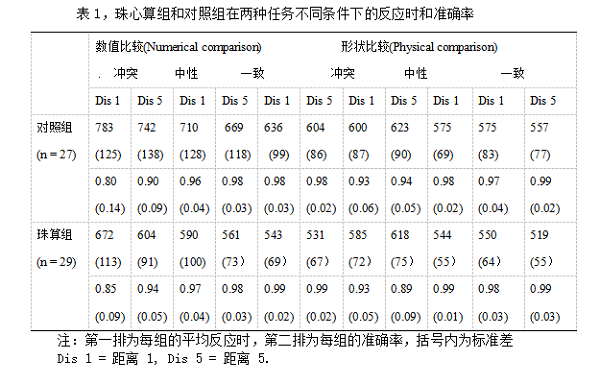
本实验中,准确率低于80%的被试被剔除(3个对照组被试和一个珠心算组的被试数据被剔除),反应时快于300ms 或慢于1200ms的数据也被剔除。只计算准确反应的反应时。从下表中可以看出珠心算组和对照组的反应时和准确率。
我们对数据进行了统计分析,首先,采用2(组别:珠心算组、对照组)× 2(任务类型:数值比较、形状比较)× 2(顺应效应:一致、冲突)× 2(距离效应:距离小、距离大)对准确率和反应时进行重复测量方差分析。发现组别、任务类型、顺应效应和距离效应在准确率和反应时上存在显著的交互作用(p<0.001)。其次,对珠心算组和对照组分别在准确率和反应时维度上进行2(任务类型) × 2(顺应效应)× 2(距离效应)重复测量方差分析。
接着用2 × 2 重复测量方差分析来考察每组被试在每种任务下的顺应效应和距离效应;其次,用双尾独立t检验考察两组间的易化效应和干扰效应;最后用双尾配对t检验考察每组被试在数值比较和形状比较时的加工速度的差异。
3.1 顺应效应
不管是在反应时(图1 a,b)方面还是准确率(图 2 c,d)方面,珠心算组和对照组在数值比较和形状比较时,顺应主效应显著,一致性条件下比冲突条件下,反应时要短。在两种任务下,顺应效应和距离效应之间都不存在交互作用。
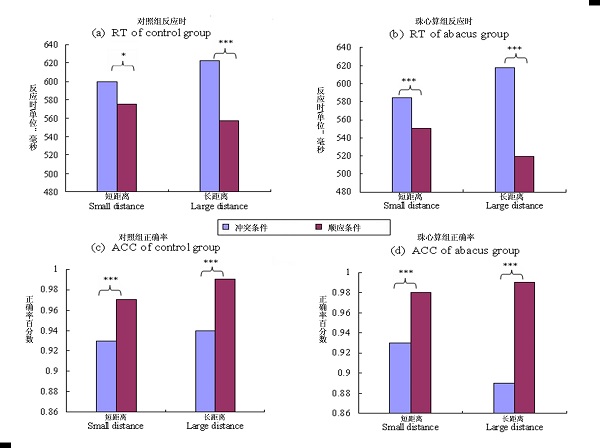
图1,珠心算组和对照组在形状比较任务中,在反应时和准确率上存在顺应效应。(* p <.05 *** p < .0001)
3.2 距离效应
反应时,珠心算组和对照组距离的主效应显著(图):1、对照组:数值比较 (F (1, 26) = 30.290, p < .0001),形状比较 (冲突条件: F (1, 26) = 6.756, p = .015; 一致性条件: F (1, 26) = 6.807, p = .015)。2、珠心算组:数值比较 (冲突条件: F(1, 28) = 37.547, p < .0001,;一致性条件: F(1, 28) = 4.709, p = .039) ;形状比较(冲突条件:F(1, 28) = 15.730, p < .0001;一致性条件: F(1, 28) = 75.690, p < .0001)。
准确率,对照组只有在数值比较的冲突条件下,距离效应显著(F (1, 26) = 36.598, p < .0001);珠心算组在两种比较任务条件下,距离效应都显著。
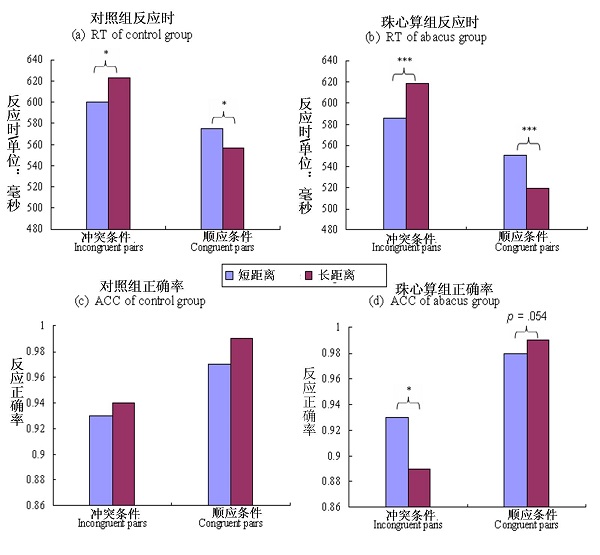
图2,形状比较任务时,在反应时上,珠心算组和对照组都存在距离效应(a,b)。在准确率上,只有珠心算组距离效应显著(d),实验组距离效应不显著(c)。(* p < .05 *** p < .0001)
3.3 干扰和易化效应
根据以往的研究,干扰率=(冲突条件下的反应时-中性条件下的反应时)/中性条件下的反应时,易化率=(中性条件下的反应时-一致性条件的反应时)/中性条件下的反应时。
分析结果发现,数值比较时,在反应时和准确率上,珠心算组和对照组在干扰效应和易化效应上没有显著差异(反应时:F (1, 55) = 1.133, p = .292;准确率:F (1, 55) = .965; p = .330, 如图3 (a), (c))。在形状比较时,珠心算组的干扰效应要显著大于对照组(反应时:t (54) = -2.578, p = .013, 准确率: t (54) = -2.841, p = .007)。
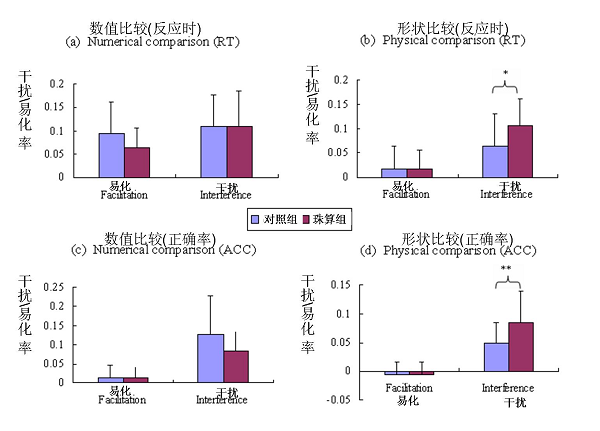
图 3 数值比较和形状比较时,干扰和易化效应。(* p < .05 ** p < .01)
3.4 形状比较和数值比较的反应速度的差异
采用双尾配对t检验来分别考察实验组和对照组,在形状比较和数值比较时的反应时的差异。珠心算组,形状比较比数值比较要快31ms,而实验组,两者之间的差异达到115ms。两种任务类型的差异,有显著的组别主效应(F (1, 55) = 10.161, p = .002, ή2 = .161,如图4所示)
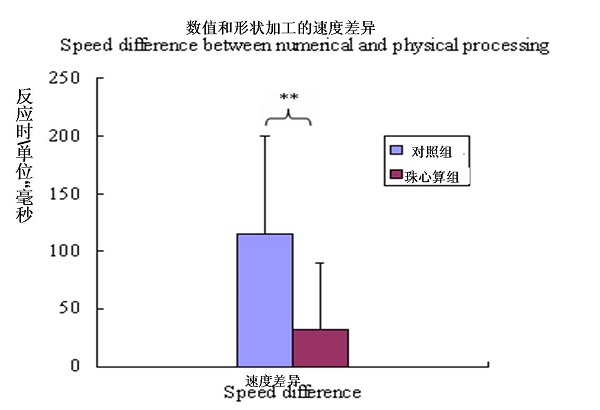
图4,数值加工和形状加工的速度差异
速度差异=数值任务中中性条件下的反应时 – 形状任务中中性条件下的反应时 (** p < .01)
4、讨论
本研究用数字Stroop范式来考察珠心算练习是否能促进儿童对符号数字数量的自动加工。对此,我们分别考察了两组被试在两种任务下(数值比较和形状比较)的顺应效应和距离效应,同时也比较了干扰效应、易化效应,以及两组儿童在形状比较和数值比较时的加工速度的差异。
我们的研究发现:1、反应时上,在形状比较时,珠心算组儿童有显著的顺应效应和距离效应,而对照组儿童只有顺应效应。2、在形状比较时,与当前任务无关的数量信息对当前任务产生了很大的干扰,这种干扰效应在珠心算组表现尤为明显。3、珠心算组在数值比较和形状比较的速度差异要比对照组小的多。
形状比较任务下的顺应效应和距离效应是检测是否对数量信息进行自动加工的重要标志。Girelli等人的研究发现较大年龄(10岁左右)的儿童,能够对阿拉伯数字的数量维度进行自动加工,不管当前的任务形式如何[5]。我们的实验结果与前人的研究比较一致,在形状比较任务中,珠心算组和对照组被试都存在顺应效应,表明与当前任务无关的数量信息都被自动的激活。
虽然,距离效应和顺应效应都能够提供充分的证据,说明珠心算儿童和普通儿童都能对符号数字的数量信息进行自动加工。但是,这两个指标还是不能揭示我们更感兴趣的问题:这两组儿童对数字自动加工的程度是否有差异。当数量信息与当前任务(数字形状大小比较)无关时,对数量信息的自动加工会影响当前知觉加工绩效[5,6]。干扰效应(干扰率)和易化效应(易化率)是检测数字自动加工程度的一个有效指标。本研究中,在形状比较任务中,珠心算组比对照组有更大的干扰效应,这表明珠心算儿童比对照组儿童对数字数量的自动化加工程度更深。然而,在本实验中,珠心算组和对照组在易化效应上并没有发现显著的组间差异。这并不是和上述结论矛盾的,产生这样的结果,可能是由于天花板效应,在形状比较任务中,珠心算组和对照组儿童反应都比较快,而且准确率都比较高。
从分析结果中(图四),我们可以看出不管是珠心算组还是实验组,形状比较比数值比较要快的多,这表明知觉加工对两组儿童来说都是优势加工。这也从另一方面反映了知觉加工的优势特性。然而,从实验结果中,我们可以看出,珠心算组任务之间的差异有减小的趋势。对珠心算儿童来说,加工数量信息仍旧比加工形状信息要难,要花更多的时间,但是两种任务之间的差异比对照组要小的多。这个实验结果为我们提供一个可能的证据:珠心算儿童对数量维度和物理知觉(形状)维度的加工优势在发生变化,数量维度的加工优势在增加。
另外,根据Dehaene的理论模型 [11],从数字比较的阶段性来看,数字比较可能包括五个阶段,前三个阶段为识别阶段,包括早期视觉加工、语言通达和语音表征;第四个阶段,呈现的数字被识别并采用一种独立与其字母或符号等视觉形式的抽象形式所表征;第五个阶段,数字才与所要求的固定数字标准进行比较并选择合适的反应。珠心算儿童有可能利用珠心算练习的特征把数量信息表征为抽象的“珠像”,其数量信息和数量的空间表征有更密切的联结。因此在数值比较任务中,比对照组更高效,在形状比较任务中,对数量信息有更加自动化的加工。
5、结论
本研究表明,珠心算组儿童和对照组儿童形成了对阿拉伯数字的数量信息进行自动加工的能力;相对来说,珠心算组儿童对数字数量自动加工的程度优于对照组儿童。但是,是什么影响了珠心算组儿童对数量信息的自动化加工?是珠心算儿童的数字空间表征发生了变化,还是其跨越了语义、语言表征阶段,直接通达了抽象表征?这些问题有待于进一步研究。
参考文献
[1] Fuson, K. C. & Hall, J. W. The Development of Mathematical Thinking (ed. Ginsburg, H. P.) 49–107 (Academic, New York, 1983).
[2] Wiese, H. Numbers, Language,the Human Mind (Cambridge Univ. Press, Cambridge, UK, 2003).
[3] Nieder, A. Counting On Neurons: The Neurobiology of Numerical Competence. Nature Reviews Neuroscience 2005, 6:117-190.
[4] Moyer R S , Landauer T K. Time required for judgments of numerical inequality. Nature, 1967, 215 (5109) : 1519.
[5] Girelli L, Lucangeli D,Butterworth B. The development of automaticity in accessing number magnitude. Journal of Experimental Child Psychology, 2000, 76: 104-122.
[6] Rousselle LNoël M-P. The development of automatic numerosity processing in preschoolers: Evidence for numerosity-perceptual interference. Developmental Psychology, 2008, 44: 544-560.
[7] Irwing P, Hamza A, Khaleefa O,Lynn R. Effects of abacus training on the intelligence of sudanese children. PersonalityIndividual Differences, 2008, 45: 694-696.
[8] Lee Y-s, Lu M-j,Ko H-p. Effects of skill training on working memory capacity. LearningInstruction, 200, 717: 336-344.
[9] Gracia-Bafalluy MNoel M-P. Does finger training increase young childrens numerical performance? Cortex, 2008, 44: 368-375.
[10] Walsh V. Cognitive neuroscience: numerate neurons. Current Biology, 2003,13: 447–448.
[11] Dehaene S, Akhavein R. Attention, automaticity,levels of representation in number processing. Journal of Experimental Psychology Learning MemoryCognition, 1995 , 21 ( 2) : 314-326.
2.2珠心算练习对儿童数量空间表征的影响
汪运起
引言
许多采用不同范式的行为实验表明,数量表征具有一定的空间特性。较小的数字表征在心理数字线(mental number line)的左侧,较大的数字表征在心理数字线的右侧。空间数字反应编码联合效应(SNARC effect)最早揭示了数量表征的这一空间特性(Dehaene, Bossini, & Giraux, 1993; Fias & Fischer, 2005)。被试在做数量比较任务、奇偶判断任务甚至数字所含音素判断任务等时,会表现出左键反应小数较快、右键反应大数较快的趋势。注意偏向效应(attention bias effect)是数量表征空间特性的又一例证。呈现一个小数会把注意引向视野的左侧,呈现一个大数会把注意引向右侧(van Galen & Reitsma, 2008)。数量表征空间特性的第三个例证是线段中分效应(line bisection effect)。被试在中分一条数字串时,数字数量的大小会影响中分点的位置(Fischer, 2001)。在中分小数组成的数字串时,被试的中分点会偏向左,而在中分大数组成的数字串时,被试的中分点会偏向右。
数量表征的空间特性也得到了脑成像实验证据的支持。数字加工和空间转换都会激活顶叶内的一些区域(Dehaene, 2003)。对健康被试的磁刺激实验表明刺激被试的左侧和右侧顶叶皮层或同时降低被试视觉空间搜索和数字比较的绩效(Gobel, Walsh, & Rushworth, 2001)。一些病理研究也进一步表明了视觉空间加工和数字加工相联系(Dehaene & Cohen, 1997)。
长期的珠心算训练使练习者形成了独特的、以“珠像(Abacus imagery)”为媒介的数字感知和计算方式,即把抽象的数字变成直观的算珠影像,并在头脑中进行类似于在算盘上的心算(Chen, et al., 2006; Hatta & Ikeda, 1988; Stigler, 1984)。也有研究表明,由于珠心算儿童在心算的过程中较多的采用了视觉空间策略,长期的珠心算练习有助于提高练习者的视觉空间工作记忆的能力和执行空间任务的绩效(Hanakawa, Honda, Okada, Fukuyama, & Shibasaki, 2003; Lee, Lu, & Ko, 2007; Tanaka, Michimata, Kaminaga, Honda, & Sadato, 2002)。我们的测试也表明,珠心算儿童在数字和字母的正背和倒背任务中的表现都明显好于对照组儿童,说明他们的工作记忆容量较对照组儿童高。
既然珠心算训练能影响练习者的视觉空间能力,而数量表征又具有一定的空间特性,那么珠心算训练是否会影响儿童数量表征的空间特性呢?其对抽象的符号数字的空间表征和非符号数字的空间表征是否有相同的影响?为此,我们采用符号和非符号数字的数量比较任务和符号数字的奇偶判断任务,来考察珠心算儿童数量表征的空间特性。
研究方法
实验对象:本研究包括30名年龄在10-12岁的身体健康的珠心算儿童(男17人,女13人,平均年龄= 11.20 ± 0.535岁)和30名同样年龄段身体健康的普通儿童(15 男,15女,平均年龄 = 11.08 ± 0.543 岁)。这两组儿童来之同一个学校、同一个年级的不同班级,接受相同的常规的小学教育,唯一不同的是珠心算组儿童每周接受3-4小时的珠心算训练,持续约3.5-4年时间。对照组没有进行珠心算训练。
刺激和方法:实验在保持日光灯照明的房间内进行,实验材料为计算机屏幕上呈现的灰底白字, 数字的形状大小分别为50号的Arial字体,呈现在17寸的纯平显示器中间,分辨率800×600,刷新频率为75赫兹,实验时被试的眼睛与屏幕中心的距离约为60cm,注视点与被试眼位处同一高度。刺激由E-Prime呈现。
实验设计与程序:实验由三部分组成,实验一,判断阿拉伯数字的数值比5大还是比5小;实验二,判断非符号(圆点)的个数比5多还是比5少。实验三,判断阿拉伯数字的奇偶性。判断刺激材料为1、2、3、4、6、7、8、9的阿拉伯数字(奇偶判断任务中也有数字5)或者圆点。对每个实验,一半实验测试项目中,采用左手-奇数/比5大/比5多、右手-偶数/比5小/比5少的判断,另一半实验测试项目采用右手-奇数/比5大/比5多、左手-偶数/比5小/比5少的判断。左右手反应顺序在被试内平衡。首先呈现500ms的注视点,然后注视点消失,在注视点的位置出现刺激目标,要求被试又快又准确的按左右键(F,J)选择准确答案,刺激目标一出现被试就可做出反应,在被试反应后空屏或延时1000ms ,然后进入下一轮试验。整个实验过程中,都要求被试注视屏幕中间的注视点。每种任务下的实验刺激随机呈现。
结果与分析
本实验中,在符号数字数量比较任务中,4名被试没有正确执行主试的要求(实验组1名,对照组3名),数据被剔除;在非符号数字数量比较任务中,2名被试没有正确执行主试的要求(实验组1名,对照组1名),数据被剔除;在符号数字奇偶判断任务中,7名被试没有正确执行主试的要求(实验组3名,对照组4名),数据被剔除。另外,每个被试错误反应的反应时被剔除,快于200ms和慢于1300ms的反应时被剔除。由于SNARC效应和距离效应反应了数量表征和空间表征的联结,我们主要统计被试在上述任务中SNARC效应和距离效应。
根据Fias等人以及Lorch和Myers的方法(Fias, 1996; Lorch RF Jr & JL., 1990),为了计算Snarc效应,全部数据经如下处理:1、计算每个被试在每个数字上的平均反应时,左右手分别计算;然后右手反应时减左手反应时,得到dRT;2、对每个被试进行回归分析,统计SNARC效应时自变量为数量大小(1, 2, 3, 4, 6, 7, 8, 9,奇偶判断任务中也有数字5),统计距离效应时自变量为呈现的刺激与5之间距离的以10为底的对数(0, 0.301, 0.477, 0.602),因变量为dRT;3、对每组被试的回归系数(包括2所得的组内每个被试的回归系数)进行one-sample T test,看其与零相比是否显著。如显著,则判断存在SNARC效应和距离效应。
实验一 阿拉伯数字数量比较任务
SNARC效应
珠心算儿童:
根据上述方法的回归分析,可以得到珠心算儿童的回归方程dRT = 45.95 -14.29 (magnitude),回归系数/斜率与零差异显著,t(28) = -3.550, p < .005(单尾),SANRC效应存在(见Fig.1a)。
对照组:
同样,可以得的对照组的回归方程dRT = 8.12 -7.10 * (magnitude),回归系数/斜率与零差异不显著,t(26) = -1.121, p >. 10(单尾),SANRC效应不显著(见Fig.1a)。
Fig.1a 阿拉伯数字数量比较任务中实验组和对照组的SANRC效应
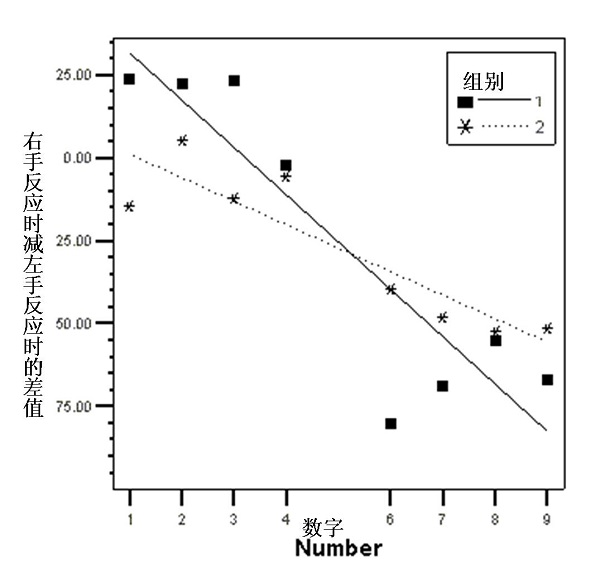
注:dRT为被试对某一呈现刺激右手反应时减去左手反应时(ms), Number为呈现的刺激(group1= 实验组,group2= 对照组,下同)
距离效应
珠心算儿童:
得回归方程mean RT = 619.70 -59.83 * (Lndistance),回归系数/斜率与零差异显著, t(28) = -6.169, p = .000(单尾),distance效应存在(见Fig.1b)。
对照组:
得回归方程mean RT = 683.27 -109.24 * (Lndistance),回归系数/斜率与零差异显著,t(26) = -10.401, p = . 000(单尾),distance效应显著(见Fig.1b)。
组间差异:
实验组(-59.83)与对照组(-109.24)的回归系数差异显著,t(54) = 3.462, p = . 001(双尾),distance效应差异显著(见Fig.1)。
Fig.1b阿拉伯数字数量比较任务中实验组和对照组的距离效应
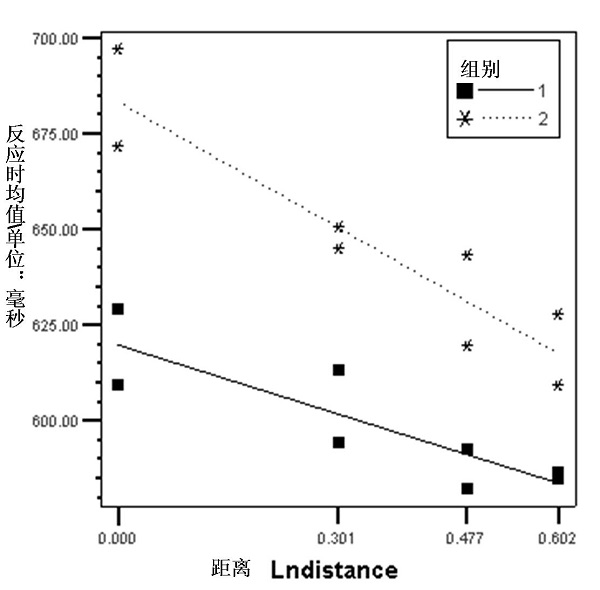
注:mean RT为被试对某一呈现刺激右手反应时与左手反应时的平均数(ms), Lndistance为呈现的刺激与5之间距离的以10为底的对数
实验二 圆点数量比较任务
SNARC效应
珠心算儿童:
得回归方程dRT = 24.20 -11.17 * (magnitude),回归系数/斜率与零差异显著, t(28) = -2.107, p <.025(单尾),SNARC效应存在(见Fig.2a)。
对照组:
得回归方程dRT = 24.01 - 12.68 * (magnitude),回归系数/斜率与零差异显著,t(28) = -2.348, p < . 025(单尾),SNARC效应存在(见Fig.2a)。
另外,两组的回归系数差异不显著,表明两组的SNARC效应差异不显著,t(56) = .199, p = .843(双尾)。
Fig.2a 圆点数量比较任务中实验组和对照组的SANRC效应
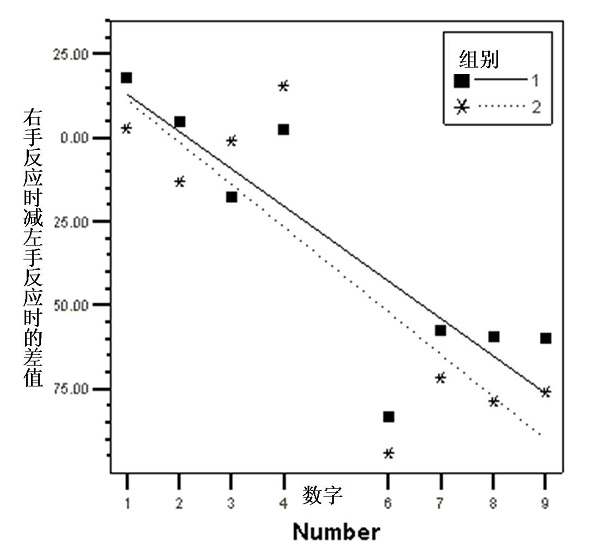
注:dRT为被试对某一呈现刺激右手反应时减去左手反应时(ms), Number为呈现的刺激
距离效应
珠心算儿童:
得回归方程mean RT = 697.04 -181.48 * (Lndistance),回归系数/斜率与零差异显著, t(28) = -17.837, p = .000(单尾),距离效应存在(见Fig.2b)。
对照组:
得回归方程mean RT = 732.02 -198.99 * (Lndistance),回归系数/斜率与零差异显著,t(28) = -10.303, p = . 000(单尾),距离效应存在(见Fig.2b)。
另外,两组的回归系数差异不显著(实验组:-181.48,对照组:-198.99),表明两组的距离效应差异不显著,t(56) = .802, p = .426(双尾)(见Fig.3)。
Fig.2b 圆点数量比较任务中实验组和对照组的距离效应
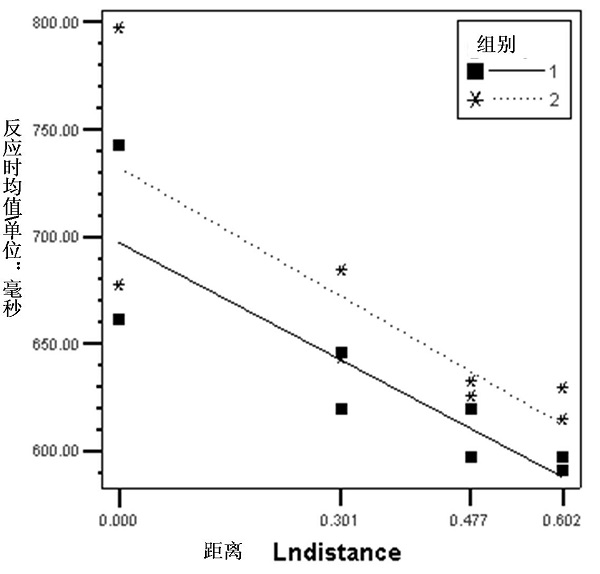
注:mean RT为被试对某一呈现刺激右手反应时与左手反应时的平均数(ms), Lndistance为呈现的刺激与5之间距离的以10为底的对数
实验三 阿拉伯数字奇偶判断任务
珠心算儿童:
得回归方程dRT = -19.28 + 0.95 * (magnitude),回归系数/斜率与零差异不显著, t(26) = 0.465, p > .25(单尾),SNARC效应不显著(见Fig.3)。
对照组:
得回归方程dRT = -18.83 - 0.25 * (magnitude),回归系数/斜率与零差异不显著,t(26) = - 0.112, p > . 45(单尾),SNARC效应不显著(见Fig.3)。
Fig.3阿拉伯数字奇偶判断任务中实验组和对照组的SANRC效应
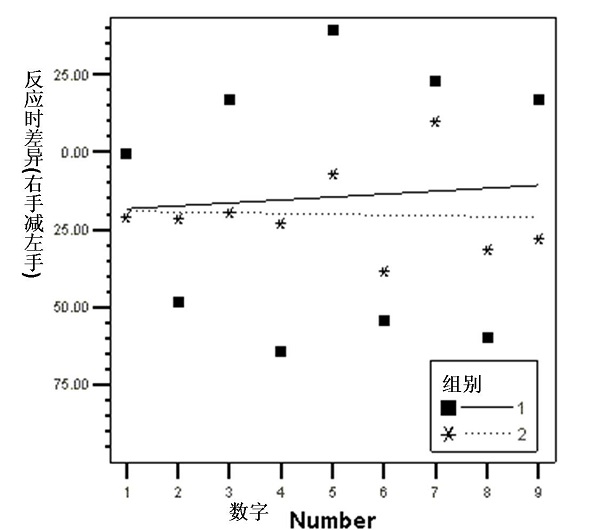
注:dRT为被试对某一呈现刺激右手反应时减去左手反应时(ms), Number为呈现的刺激
讨论
已有的研究表明,在西方,三年级的儿童在数字奇偶判断任务中即可表现出SNARC效应(Berch, Foley, Hill, & Ryan, 1999),一年级儿童即可在数字数量比较任务中表现出SNARC效应(van Galen & Reitsma, 2008),而本研究中的被试为五年级第二学期的学生,但实验组只有在数字数量比较任务中表现出SNARC效应,而对照组在数字数量比较任务和数字奇偶判断任务中均为表现出SNARC效应。这表明中国儿童出现SNARC效应的时间可能晚于西方儿童。文化因素可能是造成这一差异的原因。汉语中数字的读音特点(音节较短)使得儿童在平时的游戏和教育中即可正背数字(如12345)也可倒背数字(如54321)。这种文化因素掩盖了符号数字表征原有的空间特性,在一定程度上抵消了一部分的SNARC效应,从而延后了SNARC效应的出现时间。而在圆点数量比较任务中,不需要数字读音的参与,数量的空间特性不受上述文化因素的影响,因此两组儿童在圆点数量比较任务中都表现出了SNARC效应。当然,我们并不排除其他可能的原因对中国儿童SNARC效应出现时间的影响。
如果中国儿童SNARC效应出现较晚确实是受特定文化因素影响的结果,那么这种文化因素对珠心算儿童和对照组儿童的影响应该是相同的。但是,珠心算儿童在符号数字数量比较任务中表现出了SNARC效应,而对照组儿童在这项任务中却没表现出SNARC效应。这说明,珠心算训练可能促进了儿童数量与空间表征的联结,加速了抽象数字认知的发展。两组儿童在距离效应上的差异也印证了这一点。珠心算儿童的距离效应更接近于成年人的模式(回归线斜率小,距离效应平缓;而对照组儿童的距离效应更陡峭)。
但为什么珠心算儿童在圆点比较任务中没有表现出更强的数量与空间表征的联结呢?实验二的统计结果表明,两组儿童都表现出SNARC效应和距离效应,但组间不存在显著差异。已有的研究表明,人类至少有两种数量表征系统:符号表征和非符号表征。而珠心算的“珠像”也会是一种符号,因此珠心算练习应该对数量的符号表征影响较大,而对数量的非符号表征影响不大。实验二的统计结果证实了这一点,即珠心算练习对数量的非符号表征无显著影响。
在阿拉伯数字奇偶判断任务中,两组儿童都没表现出SNARC效应。这可能意味着奇偶判断对中国儿童来说是一项更难的任务,或者中国儿童对奇偶判断任务的加工模式或策略与西方儿童有差异。中国儿童的奇偶概念可能存储在长时记忆中。这有待于将来的实验来进一步验证。
结论
我们的研究表明长期的珠心算练习对符号数量的空间表征影响显著,但对非符号数量的空间表征无显著影响。此外,我们的研究还发现中国儿童出现SNARC效应的时间可能晚于西方儿童,并且中国儿童对奇偶判断任务的加工模式或策略可能与西方儿童有差异。
参考文献
Berch, D. B., Foley, E. J., Hill, R. J., & Ryan, P. M. (1999). Extracting ParityMagnitude from Arabic Numerals: Developmental Changes in Number ProcessingMental Representation. Journal of Experimental Child Psychology, 74(4), 286-308.
Chen, F., Hu, Z., Zhao, X., Wang, R., Yang, Z., Wang, X., et al. (2006). Neural correlates of serial abacus mental calculation in children: A functional MRI study. Neuroscience Letters, 403(1-2), 46-51.
Dehaene, S. (2003). The neural basis of the Weber-Fechner law: a logarithmic mental number line. Trends in Cognitive Sciences, 7(4), 145-147.
Dehaene, S., Bossini, S., & Giraux, P. (1993). The Mental Representation of ParityNumber Magnitude. Journal of Experimental Psychology: General, 122(3), 371-396.
Dehaene, S., & Cohen, L. (1997). Cerebral Pathways for Calculation: Double Dissociation between Rote VerbalQuantitative Knowledge of Arithmetic. Cortex, 33(2), 219-250.
Fias, W. (1996). The Importance of Magnitude Information in Numerical Processing: Evidence from the SNARC Effect (Vol. 2, pp. 95 - 110): Psychology Press.
Fias, W., & Fischer, M. (2005). Spatial representation of number Handbook of Mathematical Cognition (pp. 43-54): Psychology Press.
Fischer, M. H. (2001). Number processing induces spatial performance biases (Vol. 57, pp. 822-826).
Gobel, S., Walsh, V., & Rushworth, M. F. S. (2001). The Mental Number Linethe Human Angular Gyrus. NeuroImage, 14(6), 1278-1289.
Hanakawa, T., Honda, M., Okada, T., Fukuyama, H., & Shibasaki, H. (2003). Neural correlates underlying mental calculation in abacus experts: a functional magnetic resonance imaging study. NeuroImage, 19(2), 296-307.
Hatta, T., & Ikeda, K. (1988). Hemispheric specialization of abacus experts in mental calculation: Evidence from the results of time-sharing tasks. Neuropsychologia, 26(6), 877-893.
Lee, Y.-s., Lu, M.-j., & Ko, H.-p. (2007). Effects of skill training on working memory capacity. LearningInstruction, 17(3), 336-344.
Lorch RF Jr, & JL., M. (1990). Regression analyses of repeated measures data in cognitive research. J Exp Psychol Learn Mem Cogn., 16(1), 149-157.
Stigler, J. W. (1984). "Mental abacus": The effect of abacus training on Chinese childrens mental calculation. Cognitive Psychology, 16(2), 145-176.
Tanaka, S., Michimata, C., Kaminaga, T., Honda, M., & Sadato, N. (2002). Superior digit memory of abacus experts: an event-related functional MRI study (Vol. 13, pp. 2187-2191).
van Galen, M. S., & Reitsma, P. (2008). Developing access to number magnitude: A study of the SNARC effect in 7- to 9-year-olds. Journal of Experimental Child Psychology, 101(2), 99-113.
2.3 珠心算练习对儿童脑白质的影响
胡玉正
1引言
算盘的应用在中国已有上千年的历史,人们使用算盘来进行加、减、乘、除、甚至开方等各种运算。能熟练使用算盘的老手还有一种特别的技能,他们能在头脑中虚拟一个算盘并用其进行各种计算,这种技能也就是所谓的“珠心算”。实际上,只要经过一定量的练习,儿童也能习得珠心算的能力,中国就有很多学前儿童和小学生学习珠心算。他们学习珠心算的过程大致如下:首先学习如何操作一个实际的算盘,在熟练之后便尝试在脑海中想象算盘的形状,通过手指运动来辅助移动想象中的算盘珠子以达到操作算盘的目的,再经过若干时间的练习后就可以不需要借助手指的运动而对想象中的算盘进行操作了,到这个阶段他们便已经习得了珠心算的技能,但是珠心算者要达到熟练的程度、要进行复杂的计算(比如多位数的乘除法)还需要大量的练习。根据以前的研究,谙熟算盘操作的人其心算能力要比一般人优越,他们能以极高的精度和速度完成10位数的计算任务[Stigler 1984]。心算是一种高级认知能力,它涉及很多的认知层面,包括数字的再认、某些数学概念的加工、中间结果的临时存储等等。已有的行为实验表明珠心算主要使用的视空操作策略[HatanoOsawa 1983; HattaIkeda 1988; Stigler 1984],而普通心算使用的是基于语言的加工方法[Dehaene, et al. 1999]。功能核磁共振成像研究结果显示成人的数字工作记忆和心算过程与视空信息加工的神经资源相关[Hanakawa, et al. 2003; Tanaka, et al. 2002],而我们此前在对儿童的fMRI研究也得到了相同的结论[Chen, et al. 2006]。
到目前为止,关注珠算练习对儿童计算能力影响的研究还不太多[Chen, et al. 2006; Stigler 1984],尤其是珠算对儿童脑结构发育的影响还没有人报道过。大脑皮层的结构通常会随着特殊技能的练习发生改变[Ilg, et al. 2008],fMRI研究表明珠心算者和非珠心算者在相同的计算任务中所使用的脑区存在差异[Hanakawa, et al. 2003; Tanaka, et al. 2002],这个结果意味着珠心算作为一种独特的计算方法很可能影响了练习者的局部脑发育。本研究的目的就是为了考察经过长期的珠心算练习的儿童,其脑结构是否有别于一般儿童,如果是,那么这些变化会发生在哪些脑区。很多研究已经表明,特殊技能的长期练习会引起神经结构的变化,并且这种变化和技能的特性是紧密相关的[Bengtsson, et al. 2005; GaserSchlaug 2003; Imfeld, et al. 2009; Jancke, et al. 2009; SchmithorstWilke 2002]。就珠心算而言,在练习过程中有两个显著特点:1)无论是真实的还是想象中的算盘,算盘使用者能够同时使用双手对其进行操作;2)视空信息的加工处理在珠心算过程中发挥着至关重要的作用[Chen, et al. 2006; Hanakawa, et al. 2003; HatanoOsawa 1983; HattaIkeda 1988; Stigler 1984; Tanaka, et al. 2002]。根据珠心算练习的这两个特性我们提出这样一个假设:对于儿童,长期的珠心算练习将会引起某些脑区中白质(即连接皮层之间的神经纤维)发生改变,这些改变很可能发生在与运动和视空信息加工相关的脑区。为了检验我们的这个假设,我们在本研究中使用弥散张量成像技术(Diffusion Tensor Imaging, DTI)比较了珠心算组和对照组之间脑白质中的各向异性分数(Fractional anistropy,FA)的差异,为了获得脑白质结构变化的更多信息,我们还比较了径向扩散系数(Axial Diffusivity,AD)和横向扩散系数(Radial Diffusivity,RD)的组间差异。各向异性分数能反映白质密度和神经细胞的成熟以及髓鞘化的情况,径向扩散系数能反映两组被试在细胞成熟方面的差异,而横向扩散系数能反映两组被试在神经突触在髓鞘化方面的差异[Song, et al. 2003; Song, et al. 2002]。此外,我们还比较了两组被试在数字和字母记忆广度上的差异,并考察工作记忆容量和上述DTI指标之间的关系。
2方法
被试
珠心算组由25名健康儿童组成,平均年龄/标准差为10.48./0.58岁,年龄范围为9.61-11.58岁,其中女性10名。对照组也由25名健康儿童组成,平均年龄/标准差为10.23/0.52岁,年龄范围为8.89-11.51岁,其中女性12名。所有珠心算组的儿童所受的珠心算练习都超过3年,在练习期间他们每个星期练习3到4个小时。所有控制组的儿童均没有受过珠心算练习。被试信息参见表1。
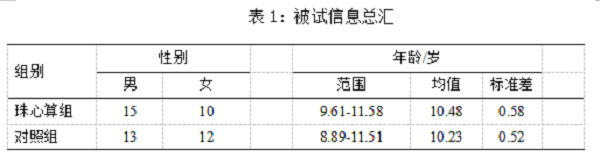
行为实验:数字/字母记忆广度测验
在数字记忆广度的测试中,由1-9组成的数字串以大约每秒一位的听觉刺激给出,被试在听完数字串的最后一位数时立即按顺序重复出该数字串。最短的数字串为2位,无论能不能成功复述听到的数字串,被试都会听到第二个相同长度的数字串,如果被试成功重复复述其中一个数字串,那么数字串的长度就增加一位,如果被试在同样长度的两个数字串都复述失败则停止测试。在被试所能达到的最大长度上,如果两个数字串都复述正确则该数字串的长度就定义为该被试的短时数字记忆广度,如果两个数字串只成功复述了其中一个则该长度减去0.5记为该被试的短时数字记忆广度。字母短时记忆广度的测量和计算方法与数字一样。
DTI图像采集
所有被试的DTI图像都在哈尔滨哈尔滨医科大学第二附属医院的Philips 3.0 T磁共振扫描仪上使用SENSE技术采集得到。成像使用单次激发的平面回波序列配合以下参数:TR/TE = 5500/78 ms, FOV = 240 mm, matrix size = 288 × 288, 50 slices, slice thickness = 3 mm, no gap, 15个梯度方向,1帧b0图像,b值800s/mm2。
DTI数据分析
预处理
DTI图像的预处理使用牛津大学的开源软件FSL(FSL, version 4.1.0; www.fmrib.ox.ac.uk/fsl, [Smith, et al. 2004]),DTI图像首先经过头动和涡流校正,然后通过解Stejskal-Tanner方程计算出扩散张量的特征值(λ1, λ2和 λ3)及特征向量,各向异性分数(FA)、径向扩散系数(AD)和横向扩散系数(RD)的定义如下:
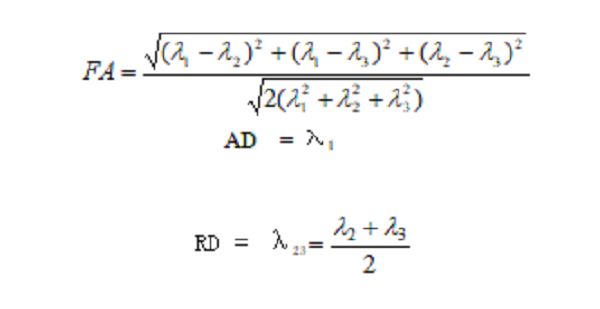
统计分析
1、行为数据的统计分析
本研究应用双样本T-检验来比较两组被试在数字和字母的工作记忆容量上的差异,并用回归分析考察数字和字母记忆容量的关系。
2、FA骨架的全脑平均值比较
脑白质的各向异性分数能反映神经纤维完整性,因为FA通常被视为白质健康程度的一个指标。为了考察珠心算练习是否对脑白质产生了显著的影响,我们使用双样本T-检验比较了两组儿童在FA骨架全脑均值上的差异,并考察FA骨架的全脑均值与数字记忆广度的关系。
3、对FA,AD,RD进行基于像素的组间比较
为了探测脑白质的局部变化,我们对全脑白质内的FA,AD,RD进行了组间比较。使用FSL提供的非参数统计程序randomise,置换步骤为5000。组间差异显著性水平设置为P<0.05,并用threshold-free cluster enhancement [SmithNichols 2009]作多重比较校正。
4、数字工作记忆广度和DTI测量指标之间的关系
为了考察被试在工作记忆广度上的表现和局部脑白质DTI指标之间的关系,我们使用了线性回归方法将DTI各指标在FA有组间差异的脑区中的均值视为因变量,将数字记忆广度视为自变量来进行研究。
3结果
3.1、行为结果
珠心算组的数字记忆广度(Digital Memory Span, DMS)和字母记忆广度(Letter Memory Span,LMS)为9.0±1.1和4.8±0.5,而控制组的分别为7.4±1.3和4.0±0.5。珠心算组在数字记忆广度上显著高于控制组(t = 5.43, P = 0.00),在字母记忆广度上也显著高于控制组(t = 4.65, P = 0.00)。此外对所有被试进行的回归分析表明:数字记忆广度与字母记忆广度是显著相关的(r = 0.53, P = 0.00)。该结果显示在图1中。
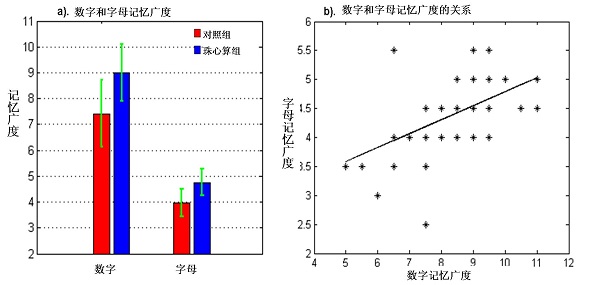
图1:珠心算组与对照组的短时数字和字母工作记忆容量。a)珠心算组在数字和字母上的短时工作记忆广度都显著高于对照组, b)个体的短时数字工作记忆广度与字母短时工作记忆广度存在显著的正相关。
3.2、图像预处理结果
图2中灰度图像表示的是所有被试的FA先与模板对齐,然后平均化的结果,绿色表示的是所有被试的FA骨架的平均值超过0.2的部分,FA阈值取0.2是为了将白质和灰质区分开,主要考察白质的变化。
3.3、FA骨架的全脑均值比较
FA骨架的全脑均值在珠心算组中为0.44 (± 0.009) ,在对照组中为 0.42 (± 0.018),FA骨架均值的分布和组内均值显示在图3a中。统计分析发现珠心算组的FA骨架全脑均值显著高于对照组 (t = 5.55, P = 0.00),对所有被试,FA骨架的全脑均值与数字工作记忆广度有显著的相关性(r = 0.45, P = 0.001)(图3b)。
3.4、FA,AD和RD的逐点分析结果
逐点进行的组间比较表明,珠心算组的FA在以下几个区域显著高于对照组(图4所示):1)左侧枕-颞联合区,2)右侧前运动区的投射,3)胼胝体前部和中前部。没有发现对照组FA比珠心算组高的脑区。珠心算组的AD与对照组没有显著差异,但是发现珠算组的RD比对照组显著低的脑区包括了几乎所有FA有组间差异的区域,此外还有辐射冠(Corona radiata)、视辐射(Optic radiation)和枕-颞联合区(Occipito-temporal junction)(图5、6所示)。
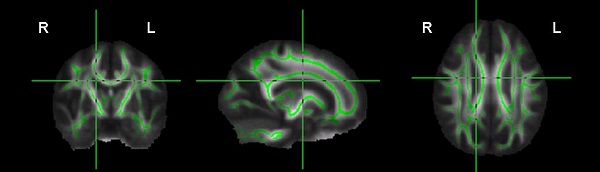
图2: 所有被试在各向异性分数(FA)上的平均值(灰度图表示),及各向异性分数的骨架图(FA skeleton, 绿色部分表示,图中R表示右侧,L表示左侧)。
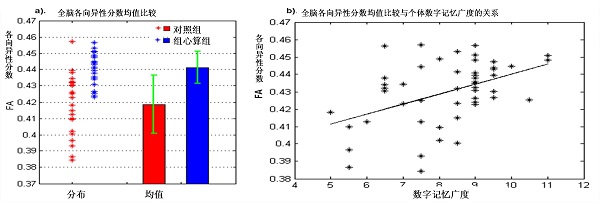
图3:各向异性分数骨架(FA skeleton)全脑均值的组间比较,a)对照组(control group)和珠心算组(AMC group)在FA骨架全脑均值的分布(星号)和均值及标准差(柱状图),珠心算组在FA骨架全脑均值上显著高于对照组;b)在所有被试中,FA骨架的全脑均值与数字短时记忆广度存在显著的正相关关系。
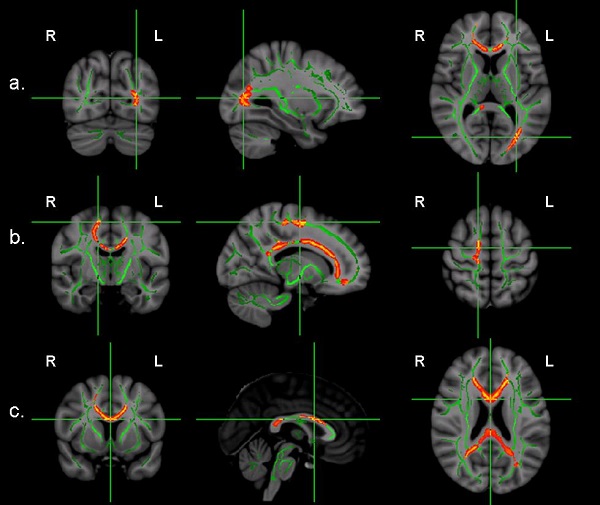
图4:基于像素的统计分析表明在以下脑区中各向异性分数FA在珠心算组显著高于对照组:a)左侧枕-颞联合区,b)右侧前运动区投射,c)胼胝体后部和中前部。没有发现对照组在FA上比珠心算组高的脑区。
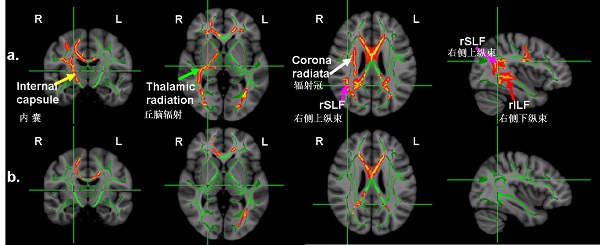
图5:基于像素的统计分析表明横向扩散系数RD在珠心算组显著低于对照组的脑区包括几乎所有FA有组间差异的脑区,此外还有右侧内囊(Internal capsule)、丘脑辐射(Thalamic radiation)、辐射冠(Corona radiata)和右侧上纵束(rSLF)及下纵束(rILF)的颞叶部分。a)表示珠心算组RD比对照组低的脑区,b)表示珠心算组FA比对照组高的脑区,两组图显示的是同一解剖结构。
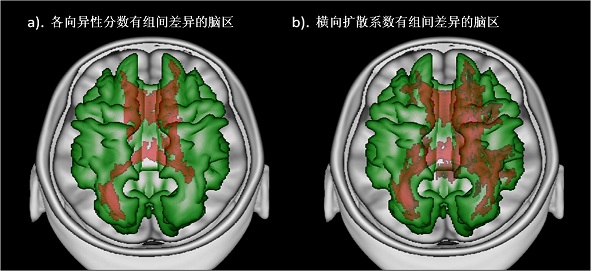
图6:FA及RD具有组间差异的脑区对照,a)表示珠心算组FA比对照组高的脑区,b)表示珠心算组RD比对照组低的脑区。通过比较可以看出RD比FA在探测脑白质差异方面具有更高的敏感性。
3.5、工作记忆广度与FA,RD及AD之间的关系
回归结果显示数字记忆广度与FA存在组间差异的区域当中的FA均值有显著的相关关系(r = 0.36, P = 0.01),与FA存在组间差异的区域中的RD均值存在显著的负相关关系(r = -0.35, P = 0.01);与FA存在组间差异的区域中的AD均值没有显著的相关关系(图7)。
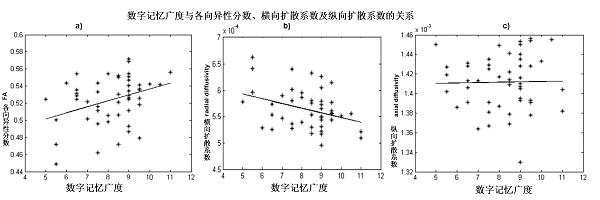
图7:短时记忆广度与DTI各指标之间的相关关系。在各向异性分数有组间差异的脑区内,a)FA的区域均值与短时记忆广度有显著的正相关关系,b)RD的区域均值与短时记忆广度有显著的负相关关系,c)AD的区域均值与短时记忆广度没有显著的相关关系。
4讨论
在本研究中,珠心算组在数字和字母记忆广度上显著高于对照组,此外对所有被试分析的结果表明数字记忆广度和字母记忆广度是正相关的。利用DTI技术,我们发现经过长期练习之后,珠心算儿童的脑白质中的各向异性分数显著高于对照组,而横向扩散系数显著低于对照组,但是径向系数在两组间没有显著差异。回归分析发现个体的工作记忆广度与局部的FA成正相关关系,与横向系数成负相关关系,而与径向系数无关。
FA骨架全脑均值结果
在本研究中,珠心算组FA的骨架全脑均值显著高于对照组。鉴于本实验中的参与者都是10岁左右的儿童,这个年龄阶段是大脑发育的重要阶段。在珠心算练习的3年里,他们的大脑为了适应珠心算操作的要求会逐渐发展成有别于对照组儿童的模式,脑的塑造是缓慢和微妙的,但是随着练习时间和强度的提高,这种微妙的改变也能积累到能够利用DTI技术观察到的程度。珠心算组的超长记忆广度很可能源于珠心算的练习,而记忆广度与FA骨架的全脑均值之间的相关关系进一步证实了珠心算练习能够改变脑可塑性的假设。
FA,RD,AD的逐点统计
逐点统计的结果表明珠心算组在左侧枕-颞联合区,右侧前运动投射通路和胼胝体前部和中部比对照组拥有较高的FA值,但是在AD方面两组间没有显著差异。在RD方面,珠心算组在FA比对照组高的区域显示出比对照组更低的RD值,另外在后丘脑投射,右侧内囊,右侧顶颞联合区也显示更低的RD。也就是说珠心算组FA的增加主要源于RD的减少。下面对这些有组间差异的脑区进行逐一讨论:
枕-颞联合区
在枕-颞联合区,有许多神经纤维经过,其中包括下纵束(inferior longitudinal fasciculus ,ILF),额枕下束(inferior fronto-occipital fasciculus ,IFOF)和视辐射(optic radiation ,OR)。ILF是连接枕叶和颞叶的主要神经纤维,能将视觉信号快速地从视皮层传输到颞叶前部[Catani, et al. 2003],同时有研究认为它与视觉的临时性记忆相关TusaUngerleider 1985。IFOF从前额叶延伸到对侧枕叶,在语义处理中具有关键的作用[Mandonnet, et al. 2007]。OR则负责将视觉信号从膝状核投射到视皮层。从这三条神经纤维的功能上我们推测枕颞联合区在视觉信号转化为语义的过程中起着整合的作用,这意味着珠心算中三种数字表征的整合—即算盘形式、语义形式及语音形式,使得枕颞联合区的白质成熟加快。
右侧前运动区通路
算盘操作者同时使用双手进行操作,这样就使得珠心算练习者相对于非珠心算练习者更多地使用了左手,这个因素可能加快右侧前运动区通路的成熟过程。此外前运动区和动态的视空间图像处理有关[Lamm, et al. 2001],研究认为在将一条视觉或者听觉命令转化为一个动作的过程中起关键作用[Passingham 1989]。还有研究发现前运动区负责语言信息和空间信息的更新[Tanaka, et al. 2005]。根据这些讨论,珠心算组前运动区通路脑白质比对照组更成熟的原因可能来自两个方面:1)珠算过程中左手的频繁使用,2)在珠心算任务中,珠心算者调用了更多的空间信息处理,而空间信息的处理主要在右脑。
胼胝体
珠心算组FA在胼胝体前部和中前部比对照组更高(图)。有研究使用DTI技术对通过胼胝体的神经纤维进行了细致的分析,通过胼胝体前部的纤维束主要连接了对侧的顶叶,枕叶和颞叶,而通过中前部的纤维则主要连接了对侧的前运动区和辅助运动区[HoferFrahm 2006]。另外来自神经影像学的研究表明左右顶叶存在分工合作的关系:左侧顶叶主要负责空间图像的产生,而右侧顶叶则负责对这些图像的操作加工[Formisano, et al. 2002]。在珠心算任务中,双侧的前运动区和顶叶后部均被激活[Chen, et al. 2006; Hanakawa, et al. 2003],根据左右顶叶的功能分割理论,珠心算过程中,表示数字的算珠的产生很可能由左侧顶叶负责,而对算珠的运算操作很可能由右脑负责,这样的功能分割就使得在珠心算过程中左右脑的信息交互十分频繁,因而负责左右顶叶和前运动区的信息传递的神经纤维使用较多,也就使其发展得更快一些。
显示RD低的其他脑区
RD在珠心算组比控制组低的脑区几乎涵盖了所有FA在珠心算组增加的脑区,此外还包括右脑的内囊(Internal),后丘脑辐射(Posterior thalamic radiation),辐射冠(Corona radiata),上纵束(SLF)和下纵束(ILF)。
后丘脑辐射与枕颞联合区是视空间注意网络的主要部分[Tuch, et al. 2005],而在颞叶部分的上纵束和下纵束主要负责将视觉信号快速地传输到颞叶前端[Catani, et al. 2003],并且在视觉临时记忆过程中起着关键作用[TusaUngerleider 1985]。视空策略在珠心算中的使用很可能就是上面提到的这些区域内髓鞘化程度增加的原因。对于内囊和辐射冠,因为内囊是连接皮层和脑干及脊髓的主要通路,而辐射冠与内囊相连,几乎所有传入传出皮层的神经信号都要经过它,因此我们推测,这两个区域FA的增加是珠心算中频繁使用右手导致的。
总而言之,RD在珠心算组的减少表现出偏侧化的形式—主要集中在右脑,这一结果有力地支持了右脑主要负责空间信息处理这个观点[Formisano, et al. 2002; Kohler, et al. 1998]。
行为数据与DTI测量指标之间的关系
工作记忆指的是在认知任务中维持和加工任务相关信息的机制或系统[Baddeley, et al. 1974; DanemanCarpenter 1980],Tanaka等人用事件相关脑功能成像(event-related fMRI)发现被试的数字短时记忆广度越长,其工作记忆相关的皮层在数字记忆任务中激活越高[Tanaka, et al. 2002], 此外,已有的行为研究表明珠算练习能够提高儿童的短时数字记忆广度[Bhaskaran, et al. 2006; Lee, et al. 2007]。在本研究中,我们发现珠心算的短时数字记忆广度显著高于对照组,并且个体的短时数字记忆广度与其主要神经纤维的FA全脑均值存在正相关的关系,进一步的分析还发现,个体的短时数字记忆广度与FA表现出组间差异的区域内FA的均值成正比,相同区域内RD成反比而与AD没有显著的相关关系。这个结果意味着FA的组间差异确实与珠心算练习相关,同时也再次印证了已有的研究结论——珠心算练习能提高儿童的工作记忆容量。
5总结
本研究考察了一组经过3年多珠心算练习的10岁左右的儿童与一组年龄、性别匹配的儿童在脑结构及工作记忆容量方面的差异。分析表明,珠心算组在短时数字记忆广度上显著高于对照组,个体的短时数字记忆广度与其脑结构存在相关关系;利用扩散弥散张量技术,我们发现珠心算组儿童在与视空信息处理相关的脑区如前运动区的神经通路、枕颞联合区及胼胝体前部和中前部显示出较高各向异性分数,这个结果表明珠心算能提高儿童的工作记忆容量,同时能加强视空信息处理相关的神经通路的发展。
参考文献
Baddeley AD, Hitch G, Gordon HB. (1974): Working Memory. Psychology of LearningMotivation: Academic Press. p 47-89.
Bengtsson SL, Nagy Z, Skare S, Forsman L, Forssberg H, Ullen F. (2005): Extensive piano practicing has regionally specific effects on white matter development. Nat Neurosci 8(9):1148-1150.
Bhaskaran M, Sengottaiyan A, Madhu S, Ranganathan V. (2006): Evaluation of Memory in Abacus Learners. Indian J Physiol Pharmacol 50(3):225-233.
Catani M, Jones DK, Donato R, ffytche DH. (2003): Occipito-temporal connections in the human brain. Brain 126(9):2093-2107.
Chen F, Hu Z, Zhao X, Wang R, Yang Z, Wang X, Tang X. (2006): Neural correlates of serial abacus mental calculation in children: A functional MRI study. Neuroscience Letters 403(1-2):46-51.
Daneman M, Carpenter PA. (1980): Individual differences in working memoryreading. Journal of Verbal LearningVerbal Behavior 19(4):450-466.
Dehaene S, Spelke E, Pinel P, Stanescu R, Tsivkin S. (1999): Sources of Mathematical Thinking: BehavioralBrain-Imaging Evidence. Science 284(5416):970-974.
Formisano E, Linden DEJ, Di Salle F, Trojano L, Esposito F, Sack AT, Grossi D, Zanella FE, Goebel R. (2002): Tracking the Minds Image in the Brain I: Time-Resolved fMRI during Visuospatial Mental Imagery. Neuron 35(1):185-194.
Gaser C, Schlaug G. (2003): Brain Structures Differ between MusiciansNon-Musicians. J. Neurosci. 23(27):9240-9245.
Hanakawa T, Honda M, Okada T, Fukuyama H, Shibasaki H. (2003): Neural correlates underlying mental calculation in abacus experts: a functional magnetic resonance imaging study. NeuroImage 19(2):296-307.
Hatano G, Osawa K. (1983): Digit memory of grand experts in abacus-derived mental calculation. Cognition 15(1-3):95-110.
Hatta T, Ikeda K. (1988): Hemispheric specialization of abacus experts in mental calculation: Evidence from the results of time-sharing tasks. Neuropsychologia 26(6):877-893.
Hofer S, Frahm J. (2006): Topography of the human corpus callosum revisited--Comprehensive fiber tractography using diffusion tensor magnetic resonance imaging. NeuroImage 32(3):989-994.
Ilg R, Wohlschlager AM, Gaser C, Liebau Y, Dauner R, Woller A, Zimmer C, Zihl J, Muhlau M. (2008): Gray Matter Increase Induced by Practice Correlates with Task-Specific Activation: A Combined FunctionalMorphometric Magnetic Resonance Imaging Study. J. Neurosci. 28(16):4210-4215.
Imfeld A, Oechslin MS, Meyer M, Loenneker T, Jancke L. (2009): White matter plasticity in the corticospinal tract of musicians: A diffusion tensor imaging study. NeuroImage 46(3):600-607.
Jancke L, Koeneke S, Hoppe A, Rominger C, Hanggi J. (2009): The Architecture of the Golfers Brain. PLoS ONE 4(3):e4785.
Kohler S, McIntosh AR, Moscovitch M, Winocur G. (1998): Functional interactions between the medial temporal lobesposterior neocortex related to episodic memory retrieval. Cereb. Cortex 8(5):451-461.
Lamm C, Windischberger C, Leodolter U, Moser E, Bauer H. (2001): Evidence for Premotor Cortex Activity during Dynamic Visuospatial Imagery from Single-Trial Functional Magnetic Resonance ImagingEvent-Related Slow Cortical Potentials. NeuroImage 14(2):268-283.
Lee Y-s, Lu M-j, Ko H-p. (2007): Effects of skill training on working memory capacity. LearningInstruction 17(3):336-344.
Mandonnet E, Nouet A, Gatignol P, Capelle L, Duffau H. (2007): Does the left inferior longitudinal fasciculus play a role in language? A brain stimulation study. Brain 130(3):623-629.
Passingham RE. (1989): Premotor Cortexthe Retrieval of Movement. Brain, BehaviorEvolution 33(2-3):189-192.
Schmithorst VJ, Wilke M. (2002): Differences in white matter architecture between musiciansnon-musicians: a diffusion tensor imaging study. Neuroscience Letters 321(1-2):57-60.
Smith SM, Jenkinson M, Woolrich MW, Beckmann CF, Behrens TEJ, Johansen-Berg H, Bannister PR, De Luca M, Drobnjak I, Flitney DE, Niazy RK, Saunders J, Vickers J, Zhang Y, De Stefano N, Brady JM, Matthews PM. (2004): Advances in functionalstructural MR image analysisimplementation as FSL. NeuroImage 23(Supplement 1):S208-S219.
Smith SM, Nichols TE. (2009): Threshold-free cluster enhancement: Addressing problems of smoothing, threshold dependencelocalisation in cluster inference. NeuroImage 44(1):83-98.
Song S-K, Sun S-W, Ju W-K, Lin S-J, Cross AH, Neufeld AH. (2003): Diffusion tensor imaging detectsdifferentiates axonmyelin degeneration in mouse optic nerve after retinal ischemia. NeuroImage 20(3):1714-1722.
Song S-K, Sun S-W, Ramsbottom MJ, Chang C, Russell J, Cross AH. (2002): Dysmyelination Revealed through MRI as Increased Radial (but Unchanged Axial) Diffusion of Water. NeuroImage 17(3):1429-1436.
Stigler JW. (1984): "Mental abacus": The effect of abacus training on Chinese childrens mental calculation. Cognitive Psychology 16(2):145-176.
Tanaka S, Honda M, Sadato N. (2005): Modality-Specific Cognitive Function of MedialLateral Human Brodmann Area 6. J. Neurosci. 25(2):496-501.
Tanaka S, Michimata C, Kaminaga T, Honda M, Sadato N. (2002): Superior digit memory of abacus experts: an event-related functional MRI study. Neuroreport 13(17):2187-2191.
Tuch DS, Salat DH, Wisco JJ, Zaleta AK, Hevelone ND, Rosas HD. (2005): Choice reaction time performance correlates with diffusion anisotropy in white matter pathways supporting visuospatial attention. Proceedings of the National Academy of Sciences of the United States of America 102(34):12212-12217.
Tusa RJ, Ungerleider LG. (1985): The inferior longitudinal fasciculus: A reexamination in humansmonkeys. Annals of Neurology 18(5):583-591.
2.4 珠心算练习对儿童执行注意的影响
耿凤基
1.引言
行为研究已表明,珠心算练习可以提高儿童的数字和空间记忆广度。并且,通过脑成像研究,研究者也找到了相应的神经基础(Hatano, Amaiwa, & Shimizu, 1987; Hatano & Osawa, 1983; Lee, Lu, & Ko, 2007; Tanaka, Michimata, Kaminaga, Honda, & Sadato, 2002)。我们之前的研究也发现,经过3年以上珠心算练习的儿童,在数字和字母的工作记忆广度上都要优于同年龄儿童。
Redick等人(2006)挑选出了工作记忆广度长和短的两类个体,让他们在电脑上完成Fan等人(2002)提出的注意网络任务。结果发现,工作记忆广度长的个体比短的个体,有更高的执行注意水平。另外,研究也发现,工作记忆的广度也会影响个体分配注意资源的能力,工作记忆广度更大的个体能够更加灵活分配注意的资源,而工作记忆广度更小的个体,在分配注意资源的灵活性上较差(Bleckley, Durso, Crutchfield, Engle, & Khanna, 2003)。
因此,我们就提出来,既然珠心算练习能够提高儿童的工作记忆广度,那么这种练习是否可以提高儿童的执行注意水平呢?是否可以提高儿童在完成执行注意任务过程中分配注意资源的能力呢?
本研究将主要基于Posner和他的同事所提出的三个注意网络任务(Fan, et al., 2007; Fan, et al., 2002; Posner & Peterson, 1990; Posner & Rothbart, 2007)来测量儿童的执行注意水平。Posner和他的同事认为注意包括三个网络:警觉、定向和执行注意网络。在本研究中,将主要关注警觉和执行注意网络。警觉是指在外界线索的提示作用下,个体反应速度提高的程度;执行注意是指个体监测和解决冲突的能力。警觉网络的神经基础涉及额叶、顶叶和丘脑等,执行注意的神经基础包括前额皮层和扣带回前部等。
Posner等人在早期的研究中认为以上提到的三个注意网络是独立的、互不相关的(Fan, et al., 2002; Rueda, Fan, et al., 2004)。但是,另外一些研究却发现警觉网络和执行注意网络是存在交互作用的(Callejas, Lupiáñz, & Tudela, 2004; Callejia, Lupiàñez, & Fumes, 2005; Fan, et al., 2009)。例如,Fan等人(2009)发现,在线索和目标的时间间隔为400ms时,警觉网络和执行注意网络就存在交互作用。表现为,在有线索时的执行注意水平显著差于没有线索时的执行注意水平。就其原因,他们认为警觉网络和执行注意网络涉及一些相同的神经基础,包括扣带回前部和额叶-顶叶联合网络。所以,在特定的时间间隔条件下,线索所引起的警觉占用了一部分用来监测和解决冲突的资源,导致当目标刺激出现时,个体就没有足够的注意资源来监测和解决冲突。本研究将采用与Fan等人(2009)研究中所涉及的类似范式,来检验当存在资源竞争的时候,实验组和控制组儿童在执行注意资源的分配及执行注意水平上是否存在差异。
我们的研究包括三个假设:首先,实验组儿童的执行注意能力优于控制组儿童;其次,对控制组儿童而言,资源竞争会损害他们的执行注意能力,对实验组儿童,资源竞争不会损害他们的执行注意能力;第三,当存在资源竞争的时候,实验组儿童能够更加灵活地分配注意资源。
2.研究意义
针对珠心算练习,大部分行为研究都在关注珠心算练习对儿童的数学能力的影响,例如数字工作记忆和心算技能。最近,我们研究小组发现珠心算练习会使儿童对数字形成自动加工。此外,还考察了珠心算练习对儿童脑可塑性的影响,发现长期的珠心算练习会影响儿童的脑结构。
就珠心算的练习效应来说,研究者逐渐关注这种练习在影响儿童数学能力的同时,是否能够迁移到儿童的其它能力上。例如,行为和脑成像研究都表明,珠心算练习可以提高儿童数字和空间工作记忆的广度。工作记忆与个体的注意控制能力密切相关。如果我们的研究能够检测到珠心算练习可以提高个体的执行注意水平,那么这种练习就可以应用到对特殊儿童的练习中,以改善这些儿童的执行注意能力。例如,研究发现,焦虑会损害个体的执行注意能力(Bishop, 2009)。如果珠心算练习可以改善儿童的执行注意能力,那么将来这种练习就可以应用到焦虑儿童的执行注意能力的练习当中去。
3.研究方法
3.1被试
所有被试来自黑龙江省七台河市某小学。实验组的被试已接受3年以上的珠心算练习,控制组儿童从来没有接受过珠心算练习。两组儿童在年龄、性别和智商上都是匹配的。
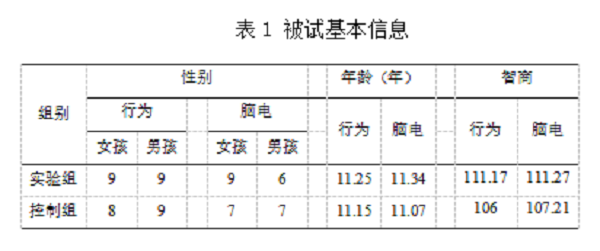
3.2研究范式
图1 儿童注意网络任务
在本研究中所采用的范式,是基于Rueda等人(2004)和Fan等人(2009)的研究范式改进而来的。首先,在屏幕上呈现一个加号(+),持续时间介于400-1200ms之间,然后出现线索,有两种类型:一种是50HZ、持续时间为50ms的纯音;另外一种是没有线索,屏幕上只出现50ms的加号(+)。之后,时间间隔100ms或者 400ms后目标出现。目标包含两种类型的刺激:冲突刺激,即中间小鱼头的朝向与旁边小鱼头的朝向完全相反;无冲突刺激,所有小鱼头的朝向都一致。让被试对中间这条小鱼头的朝向进行反应,如果朝向左边的话,就按‘F’键,如果朝向右边的话,就按‘J’键。最大的反应时间窗为1700ms,之后小鱼就会消失,进入下一个trial。
每个被试需要完成一个练习阶段和3个正式阶段。练习阶段,主试会给予儿童鼓励和支持。当正式开始之后,主试就不给予任何反馈。练习阶段持续2分钟,每个正式阶段持续4分钟。每个阶段共有96个trial。因此,每种条件下,有36个trial。
儿童在电脑上完成此任务范式的同时,我们同时采集他们的脑电数据。
4.行为结果的分析及讨论
4.1行为结果的分析方法
以线索(有线索,无线索)和线索-目标时间间隔(100ms, 400ms)为组内变量,组别(实验组,控制组)为组间变量,每种条件下的冲突得分为因变量,进行重复测量方差分析。如果能检测组别或者组别和其它变量的交互效应,再运用独立样本t检验或配对样本t检验的方法来进行事后检验。
4.2 行为结果的讨论
重复测量方差分析表明,线索-目标时间间隔和组别之间存在接近显著的交互效应(F (1,31) = 3.87, p = 0.058),线索的主效应不显著(F (1,31) = 2.67, p = 0.112)。 但事后检验发现,在100ms和400ms两种条件下,两组在执行注意的得分上都没有显著差异。因此,从这个结果上,我们只能初步得出结论认为,实验组和控制组儿童在执行注意上的差异,可能与线索-目标之间的时间间隔存在相关。我们进一步检验发现,对实验组儿童来说,他们在短间隔(100ms)条件下的执行注意优于在长间隔(400ms)条件下的执行注意(t (17) = 1.73, p = 0.103)。但是,对控制组儿童,他们的执行注意水平和刺激-目标之间的时间间隔没有关系。在将来的研究中,我们会在线索和目标刺激之间取更多的时间间隔点,进一步考察时间间隔如何影响实验组儿童的执行注意水平。
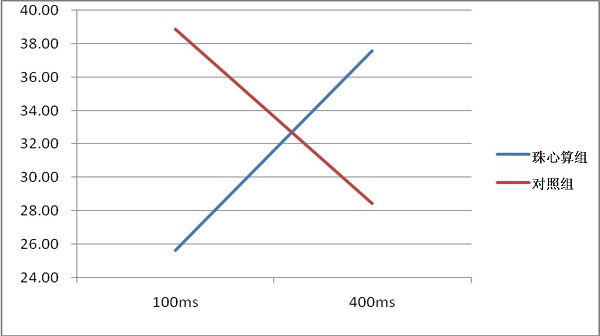
图2. 时间间隔与组别的交互作用
采用配对样本t检验,进一步分析表明,对控制组儿童,在400ms条件下,在有提示线索时的执行注意得分显著高于没有提示线索时(t (16) = 2.28, p = 0.037)。 这个结果支持了我们的第二个假设,即在存在资源竞争的时候,这会损害控制被试的执行注意水平,但是对实验组儿童而言,可能由于它们更擅长于进行资源的分配,因此资源竞争并不会损害他们的执行注意水平。
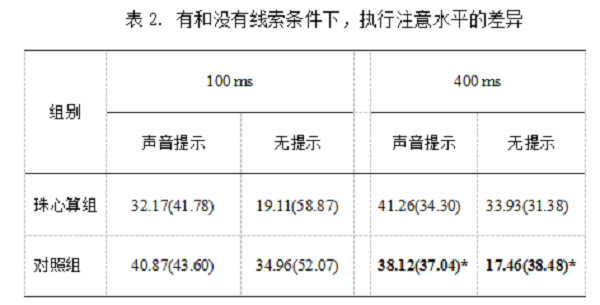
5.脑电结果的分析及讨论
5.1脑电成分的选择
基于前人的文献,及本研究中数据的总体波形,我们选择了三个脑电成分来进行分析,它们分别是N2、P300和LPC。N2是在250ms-400ms时间出现的一个负走向的成分,通常它与对冲突刺激的监测存在相关(Jonkman, 2006; Rueda, Posner, Rothbart, & Davis-Stober, 2004),主要分布在前额区域。P300与对优势反应或者无关刺激的抑制有关(Jonkman, Lansbergen, & Stauder, 2003),主要分布在顶叶和枕叶区域附近。LPC是一种在晚期出现正走向的成分,一般来说,它只在儿童的实验中才会被检测到,它与对冲突刺激的解决存在相关(Rueda, Posner, et al., 2004),也主要分布在额叶区。
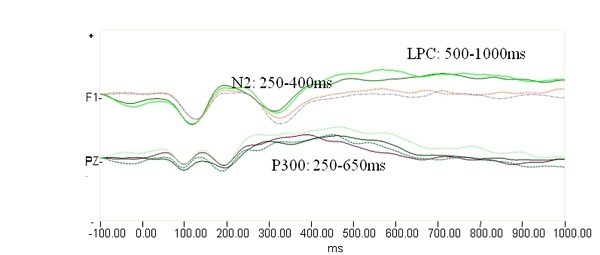
图3. N2, P300和LPC
5.2差异值
有些研究为了测量个体在有冲突刺激和没有冲突刺激两个条件下所使用资源的差异,就计算N2、P3和LPC在冲突和非冲突(冲突-无冲突)条件下幅值的差异值(Dennis & Chen, 2009)。差异值越大,表明相对于非冲突条件,个体在冲突条件下投入的注意资源越多。
5.3分析方法
对N2、LPC和P300差异值,以线索类型(有线索,无线索)和线索-目标的时间间隔(100ms,400ms)为组内变量,组别(实验组,控制组)为组间变量,进行重复测量方差分析。
如果发现组别的主效应或者与其它变量的交互效应,就采用t检验的方法来进行事后检验。
5.4脑电结果及讨论
5.4.1 N2差异差异值
重复测量方差分析发现,在额区有多个电极上存在线索与组别的交互效应(p < 0.05),这些电极包括:AF3、F1、F2、F3、F4、F5、F7、FC1、FC2、FC3、FC4、FC6、FCZ、FT8、FZ。
采用独立样本t检验发现,在没有线索时,在额区某些电极上(AF3、F1、F3、F4、F5、F7、FC1、FC2、FC3、FC4、FC6、FCZ、FT8),组别有显著的主效应(p < 0.05),即实验组比控制组投入更多的资源来监测冲突。
配对样本t检验发现,线索-目标的时间间隔为100ms时:实验组儿童在有线索时,用来监测冲突的资源显著减少(FC1、FT8);控制组儿童在有线索时,用来监测冲突的资源显著增加(FC6)。
P300差异值
重复测量方差分析发现,在顶枕区附近有多个电极存在线索与组别之间的交互作用(p < 0.05) (CP1、CP3、CP5、CPZ、O1、O2、P2、P4、P7、PO4、PO6、PO8、PZ、TP7、TP8),线索-目标时间间隔的主效应(p < 0.05) (O1、 O2、P4、PO4、PO6、PO8) ,以及线索-目标时间间隔与组别之间的交互作用(p < 0.05) (O1、 O2、PO4、PO6、PO8)。
独立样本t检验发现,在没有线索和线索-目标时间间隔为100ms的条件下,控制组比实验组投入更多的资源进行反应抑制(CP1、CPZ、O1、O2、P2、P7、PO4、PO6、PO8、PZ、TP8)。在有线索的条件下,实验组比控制组投入更多的资源进行反应抑制(CPZ、 CP5、TP7)。
配对样本t检验发现,100ms间隔条件下,在有线索时,实验组儿童用来进行反应抑制的资源增多(O1、OZ、TP8),控制组儿童用来进行反应抑制的资源减少(CP5)。400ms间隔条件下,在有线索时,实验组儿童用来进行反应抑制的资源增多(TP7)。
LPC差在异值
重复测量方差分析表明,在额区的多个电极上,线索与组别之间的存在交互作用(p < 0.05) (AF3、F1、F2、F3、F4、F5、F6、F7、F8、FC1、FC2、FC3、FC4、FC5、FC6、FCZ、FT7、FT8、FZ)。
独立样本t检验发现,在有线索和线索-目标间隔为100ms的条件下,实验组比控制组投入更多的资源解决冲突(F7、FT7)。在没有线索和线索-目标间隔为400ms的条件下,控制组比实验组投入更多的资源解决冲突(FC1、FC3)。
配对样本t检验发现, 100ms间隔条件下,在有线索时,控制组儿童用来进行冲突解决的资源减少(F7、FT7)。400ms间隔条件下,在有线索时,实验组儿童用来进行冲突解决的资源增多(F7、FC1、FC3、FC5、FT7)。
6.讨论
当线索-目标的时间间隔为100ms时,有线索比没有线索的条件下,控制组儿童用来监测冲突的资源增加,但投入解决冲突和反应抑制的资源减少;实验组儿童用来监测冲突的资源减少,但投入反应抑制的资源增多。此结果可能可以用来部分解释行为结果1。但还需开展进一步的研究来探讨线索-目标时间间隔的长度如何影响两组儿童在执行注意水平上的差异。
当线索-目标的时间间隔为400ms时,有线索比没有线索的条件下,实验组儿童用投入反应抑制和冲突解决的资源都增多。 此结果可以用来支持行为结果的发现,即在400ms间隔条件下,控制组有线索时的冲突得分显著高于没有线索时的冲突得分,但是这种差异在实验组中没有发现。
以上结果充分支持了这样的观点:实验组和控制组儿童在分配注意资源的灵活性上存在差异,实验组儿童的能力优于控制组儿童。
7.结论
实验组和控制组儿童在执行注意水平上存在差异,但这种差异与线索-目标之间的时间间隔存在相关。
一定程度的资源竞争会损害控制组儿童的执行注意,对实验组儿童的执行注意没有影响。
实验组儿童分配注意资源的灵活性优于控制组儿童。
参考文献
Bishop, S. J. (2009). Trait anxietyimpoverished prefrontal control of attention. Nat Neurosci, 12(1), 92-98.
Bleckley, M., Durso, F., Crutchfield, J., Engle, R. W., & Khanna, M. (2003). Individual differences in working memory capacity predict visual attention allocation. Psychonomic Bulletin & Review, 10(4), 884-889.
Callejas, A., Lupiáñz, J., & Tudela, P. (2004). The three attentional networks: On their independenceinteractions. BrainCognition, 54, 225-227.
Callejia, A., Lupiàñez, J., & Fumes, M. J. (2005). Modulations among the alerting, orientingexecutive control networks. Experimental Brain Research, 167, 27-37.
Dennis, T. A., & Chen, C.-C. (2009). Trait anxietyconflict monitoring following threat: An ERP study. Psychophysiology, 46(1), 122-131.
Fan, J., Byrne, J., Worden, M. S., Guise, K. G., McCandliss, B. D., Fossella, J., et al. (2007). The relation of brain oscillations to attentional networks. The Journal of Neuroscience, 27(23), 6197-6206.
Fan, J., Gu, X., Guise, K. G., Liu, X., Fossella, J., Wang, H., et al. (2009). Testing the behavioral interactionintegration of attentional networks. BrainCognition, 70(2), 209-220.
Fan, J., McCandliss, B. D., Sommer, T., Raz, A., & Posner, M. I. (2002). Testing the efficiencyindependence of attentional networks. Journal of Cognitive Neuroscience, 14(3), 340-347.
Hatano, G., Amaiwa, S., & Shimizu, K. (1987). Formation of a mental abacus for computationits use as a memory device for digits: A developmental study. Developmental Psychology, 23(6), 832-838.
Hatano, G., & Osawa, K. (1983). Digit memory of grand experts in abacus-derived mental calculation. Cognition, 15(1-3), 95-110.
Jonkman, L. M. (2006). The development of preparation, conflict monitoringinhibition from early childhood to young adulthood; a Go/Nogo ERP study. Brain Research, 1097(1), 181-193.
Jonkman, L. M., Lansbergen, M., & Stauder, J. E. A. (2003). Developmental differences in behavioralevent-related brain responses associated with response preparationinhibition in a go/no go task. Psychophysiology, 40, 752-761.
Lee, Y.-s., Lu, M.-j., & Ko, H.-p. (2007). Effects of skill training on working memory capacity. LearningInstruction, 17(3), 336-344.
Posner, M. I., & Peterson, S. E. (1990). The attention system of the human brain. Annual Review of Neuroscience, 13, 25-42.
Posner, M. I., & Rothbart, M. K. (2007). Research on attention networks as a model for the integration of psychological science. Annual Review of Psychology, 58, 1-23.
Redick, T. S., & Engle, R. W. (2006). Working memory capacityattention network test performance. Applied Cognitive Psychology, 20(5), 713-721.
Rueda, M. R., Fan, J., McCandliss, B. D., Halparin, J. D., Gruber, D. B., Lercari, L. P., et al. (2004). Development of attentional networks in childhood. Neuropsychologia, 42, 1029-1040.
Rueda, M. R., Posner, M., Rothbart, M., & Davis-Stober, C. (2004). Development of the time course for processing conflict: an event-related potentials study with 4 year oldsadults. BMC Neuroscience, 5(1), 39.
Tanaka, S., Michimata, C., Kaminaga, T., Honda, M., & Sadato, N. (2002). Superior digit memory of abacus experts: an event-related functional MRI study. NeuroReport, 13(17), 2187-2191.
2.5 珠心算练习对儿童精算估算的影响及其神经机制的研究
陈飞燕
1、引言
Albert Einstein 曾经说过他几乎不以语言文字的方式思考,而是像放电影一样用图画般的想象力来思考问题。也有很多数学家表示他们有类似的思考方式,但也有人强调语言或者其他符号系统在数学思维中的重要性。那么在数字认知加工中,语言和视觉空间起到什么作用呢?Dehaene等人[1-3]认为,在初等数学领域,至少包括两种数字的表征方式,分别是语言表征和非语言视觉空间表征。语言表征系统用来存储一些算术知识和基本规则。非语言表征系统用来表示数量信息。基于此,他们提出,精算是基于语言表征的,估算是基于视觉空间表征的[1-3]。
为了证实他们的假设,Dehaene等人[1]进行了一系列的研究,首先在一项训练研究中,俄、英双语被试在一种语言条件下分别进行精算与估算练习,随即在另一种语言条件下进行考察,结果发现,精算表现出明显的语言依赖性,而估算则很容易实现语言间的迁移。这可能是由于精算更多使用了语言表征,而估算则主要使用非语言的表征。接着Dehaene等人[1] 对7名法国成人被试进行了的fMRI研究。结果发现,估算比精算更多地激活两侧顶叶(特别是顶内沟)、右侧前楔叶、两侧中央沟等脑区,这些区域更多地与数字表征、视觉空间加工及手指运动等有关。而精算比估算更多地激活了左侧的脑区,包括额下回、楔前叶、扣带等区域,右侧的顶枕沟等脑区也有激活。这些区域,特别是左侧额下回更多的与语言加工有关。他们的fMRI及之后的fMRI和ERP研究[1,3]进一步证实了之前的假设,即精算更多地激活了与语言过程相关的区域;估算更多地激活了与视觉空间加工相关的区域。Zago等人[4]的研究也支持了Dehaene等人的假设,表明数字心理表征更多与空间、运动等功能存在密切关系。最新发表在《Science》上研究论文也提示心算和空间编码是密切相关的[5]。
目前对数学计算的脑机制,特别是对精算估算的脑机制的研究都集中在成人被试、计算有障碍的病人[6]或者脑损伤病人身上,对于正常儿童的数学认知发展的研究多采用行为学测试方法[7],很少有用影像技术来探索儿童的数学计算的脑机制[8]。而了解儿童数学能力的发展变化,掌握儿童数字认知的脑机制的发展规律,对于因材施教,进行有效的数学学习和教育尤为重要。其中一个很重要的科学问题是儿童是否存在独特的精算估算加工模式?语言表征和视觉空间表征分别在精算、估算加工中起到怎样的作用。其次,早期特殊的数学学习经验, 如珠心算训练,是否会影响儿童的精算、估算加工机制?
本研究旨在考察两方面的内容,一、儿童和成人是否有相同的精算、估算神经机制;二、珠心算练习是否会影响儿童精算、估算的脑机制。为此,我们提出以下假设:一、儿童的精算、估算脑机制可能与成人的不完全一致。因为10岁左右的儿童,虽然已经掌握了基本的加减乘除的规则,但是对计算策略的应用还不熟练,在精算和估算任务中,可能两种计算策略都会参与加工。特别是估算时,语言表征和视觉空间表征可能都会有参与。与精算相比较,估算任务对他们来说可能更难,需要更多注意资源的参与。基于珠心算的特点,我们认为,珠心算练习可能会影响儿童的精算、估算的脑机制。一方面,珠心算练习可能促进了他们在计算方面的能力,完成相同任务,他们需要的资源可能比对照组会更少些。另一方面,珠心算儿童在数字加工时,可能会更多地依赖视觉空间表征,珠心算儿童的估算加工可能是一种结果精确、加工机制与传统估算类似的精算,即精算和估算的加工机制是相似的。
因此,我们预期:一、在fMRI实验中,普通儿童在精算和估算中都有语言区和顶叶区域的激活,估算比精算激活更多的脑区,这些脑区主要集中在前额叶背外侧、两侧顶叶及扣带回;二、珠心算儿童由于掌握了珠心算加工的技巧,他们进行精算和估算的机制是相似的,参与脑区可能会集中在两侧顶叶及前额叶背外侧皮层,语言区域的激活较少;三、不管是精算任务还是估算任务,对照组的脑活动区域及活动强度会大于珠心算组,主要差异会出现在左侧语言区及与执行功能相关的前额叶的区域。
2、研究方法
实验对象:本研究包括20名身体健康珠心算儿童(男11人,女9人)和19名身体健康的普通儿童(男10人,女9人),年龄在9岁7个月到11岁4个月之间。这两组儿童来自同一个地区、同一个年级的不同学校,接受相同的常规小学教育,唯一不同的是珠心算组儿童每周接受2.5-3小时的珠心算练习,持续约3.5-4年时间。对照组没有进行珠心算练习。
刺激和方法:
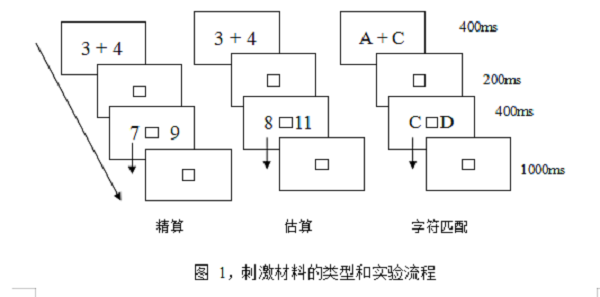
实验设计范式为:数字精确计算、数字估算和匹配任务(如图1所示)。实验刺激材料如下图所示。加数为1-9的数字,和的范围3-17,剔除类似2+2、6+6这样的配对。在精算中,有两个备选答案,一个是正确结果,另一个与正确结果至少差2。在估算中,一个选项与正确答案差1,另一个至少差4。匹配任务为字母匹配,数字被大写字母(A-F)代替。被试分别用食指按左右键反应,一半任务需要按左键反应,一半任务需要按右键反应。每12个刺激任务(trial)组成一个block,每个block之间有16秒的静息。静息状态下,要求被试注视屏幕中间的注视点。每个block开始有4秒的提示,提示任务的类型。每个被试完成两个序列的扫描(two sessions),两次扫描的刺激顺序分别为:精算-估算-字符-精算-字符-估算,估算-字符-精算-字符-估算-精算,两次扫描的刺激顺序在被试间平衡。
被试通过安置在头顶上方的反光镜,看到投射在屏幕中间的刺激材料。磁场外的电脑同步记录被试的反应。实验刺激程序用E-prime编制。刺激与扫描同步。
数据采集:
本实验是在GE 3.0T 的MRI机器上完成的。功能磁共振成像参数分别为:轴状位扫描,TR=2000ms,TE=30ms, 33层,采集矩阵 64×64,翻转角(FA)=90度,FOV =230 x 230 mm,层厚=4mm,层间距=1 mm。
数据分析:
行为数据:分别计算在精算、估算和符号比较时的准确率和平均反应时。
剔除准确率低于60%的被试。计算平均反应时时,只提取反应准确的数据,且剔除小于200ms,大于1200ms的数据。
fMRI数据:用SPM5进行常规的预处理,包括剔除前三个时间点的图像,然后进行时间序列矫正(slice timing)、头动矫正(realign)、空间标准化(Normalization,3mm×3mm×3mm)和空间平滑(smooth,半高宽= 6mm)。
我们首先对每个被试进行分析,考察个体在精算(精算-静息)、估算(估算-静息)、符号比较(符号任务-静息)及精算-符号比较、估算-符号比较等条件下的脑活动情况。然后进行二次分析,分别考察两组儿童在精算和估算时的脑活动情况,以及在精算时两组儿童脑活动的差异、估算时两组儿童脑活动的差异。
3、结果
行为数据结果
通过分析,我们发现在准确率上,珠心算组和对照组组别主效应显著((F (1, 1) = 6.267, P<0.05),任务的主效应也显著((F (1, 2) = 13.418, P<0.001);在反应时上,组别主效应((F (1, 1) = 6.267, P<0.05)和任务的主效应((F (1, 2) = 28.629, P<0.001)也都显著。在字符比较时,珠心算组和对照组在准确率上没有显著差异。从图2可以看出,对两组被试来说,估算的准确率低于精算,且反应时比精算要长的多,也就说估算的任务难度要比精算大。
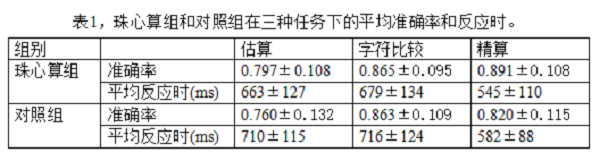
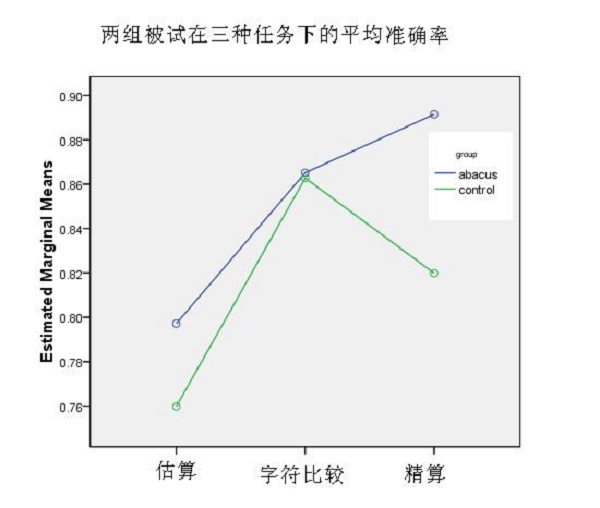
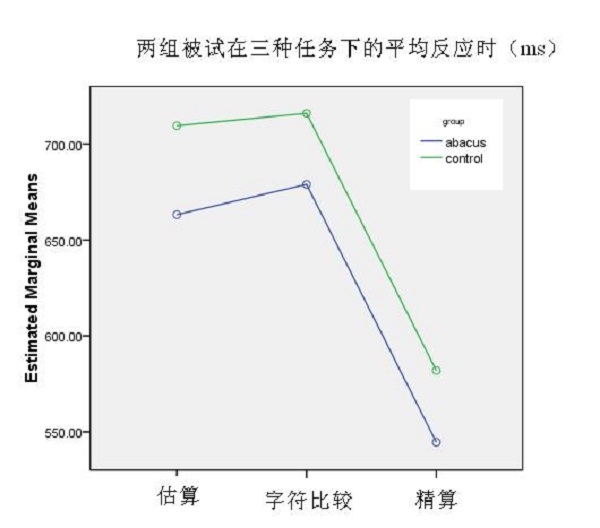
图2 珠心算组和对照组在三种任务下的平均准确率和反应时
(珠心算组--蓝色线条,对照组--绿色线条)
fMRI数据结果
珠心算组和对照组在计算任务下的激活情况
图3分别表示珠心算组在估算(A)和精算(B),对照组在估算(C)和精算(D)时脑活动的情况。值得注意的是,图3的脑激活模式是采用精算-静息或估算-静息的分析方法。采用这样的分析方法,有以下两方面的原因。一、在分析中,我们发现如果采用计算任务-字符比较的分析方法,在精算-字符的情况下,没有发现相应的激活脑区。产生这样的结果,可能是因为对儿童来说,字符比较不是一个简单的任务,一方面需要进行语义/语音的加工,另一方面还要有视觉空间加工的参与,另外还有记忆、比较、选择等多种复杂的加工过程。因此对于本实验来说,字符比较任务不是理想的对照任务(或者基线任务)。二、在本实验中,我们更加关注精算和估算的差异,并且两种任务在同一个扫描序列中,可以进行直接比较,故可以不考虑字符任务的激活情况。在图3中,我们发现珠心算组在两种任务下有相同的激活区域,包括两侧顶叶、前额叶的中部(MPFC)/辅助运动区(SMA)、额叶背外侧(延伸至额下回)、两侧脑岛、丘脑及枕叶。对照组除了有上述脑区激活外,小脑也有明显的激活。
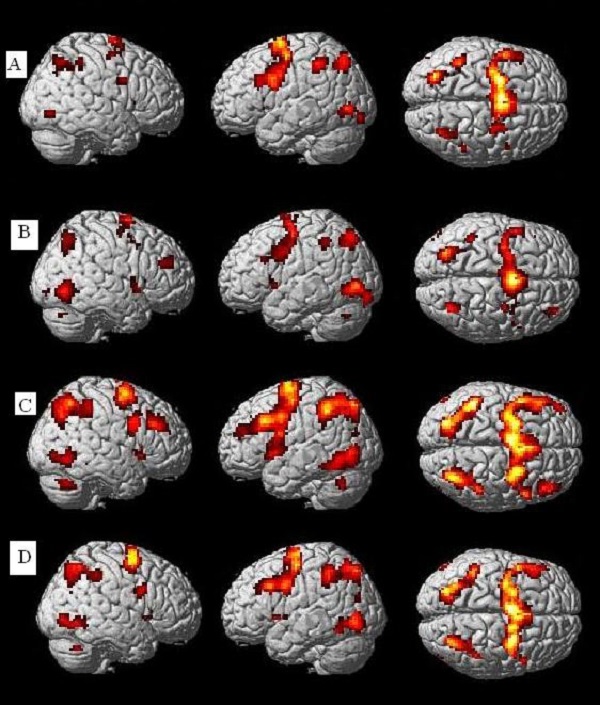
图 3, A、B分别表示珠心算组估算(估算-静息)、精算时激活的脑区;C、D分别表示对照组估算、精算时激活的脑区(p<0.001,cluster>10,uncorreceted).
珠心算组和对照组在精算估算时的差异
珠心算组,精算和估算任务比较时((精算-静息)-(估算-静息))或者((估算-静息)-(精算-静息)),在阈值(p<0.001,cluster>20 voxels,corrected)情况下没有显著差异,若采用(p<0.005,cluster>27 voxels,corrected),估算任务下会激活更多的脑区包括左侧额中回(X,Y,Z=-24,3,63)和左右两侧中央沟前回/额下回(X,Y,Z =-48,3,30;54,9,27)。对照组,在精算-估算时,没有发现激活。在估算-精算时((估算-静息)-(精算-静息)),发现有些脑区,在估算任务下有更多的激活。这些脑区主要包括辅助运动区(SMA),两侧额中回,左侧额下回(接近Broca区)及两侧顶下小叶(左侧的激活区域延伸至楔前叶,右侧延伸至角回)(如图 4 所示,p<0.001,cluster>20,corrected)。
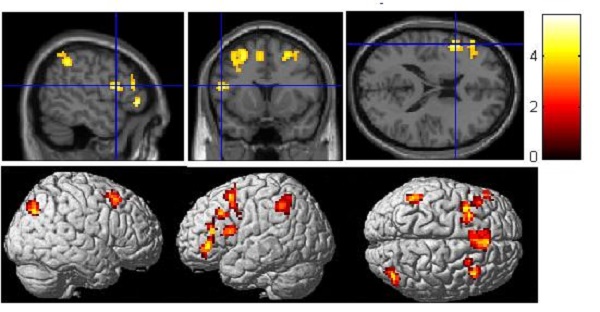
图 4 对照组估算比精算激活更多的脑区(p<0.001,cluster>20,corrected)
珠心算组和对照组之间的差异
估算时,珠心算-对照组,主要集中在前额叶的中部(MPFC)、扣带回的后部、两侧的外核(Extra-Nuclear)及左侧的角回,这些脑区基本上在默认活动网络内,可能是由于负激活的差异引起的。对照组-珠心算组,激活的脑区主要集中在左侧语言区(额下回)、左右两侧脑岛、右侧额上回、前额叶的中部(MPFC)/辅助运动区(SMA)、左侧顶上小叶及小脑部分(图5)(p<0.005,cluster>27voxels,corrected)。
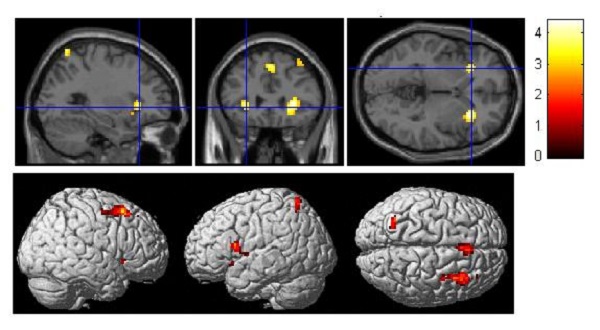
图5 估算时对照组比珠心算组激活更多的脑区(p<0.005, cluster>27voxels,corrected)
精算时,珠心算组-对照组,激活的脑区主要集中在前额叶的中部(MPFC)、扣带回的后部、两侧的外核(Extra-Nuclear)、两侧的角回、丘脑及两侧的海马、海马旁回,这些脑区也基本上在默认活动网络内,可能是由于负激活的差异引起的。对照组-珠心算组,激活的脑区在左侧顶叶,包括顶下小叶和缘上回(Supramarginal gyrus)(X,Y,Z =-33,-51,36,p<0.005,cluster>27voxels, corrected)。
4、讨论
珠心算组儿童在精算、估算任务下,脑区的激活没有显著的差异;而对照组在两种任务下,有较大的差异,特别是在估算任务下有更多的脑区参与活动。实验结论和我们的假设相吻合。实验结果表明,长期的珠心算练习,可能会促进儿童的数学计算能力,在精算和估算任务中可能采取相同的策略。对照组在估算任务中,两侧顶叶的脑区有更明显的激活,这和成人的研究结果比较一致[1,3],即估算加工可能更多的采用非语言的视觉空间的策略。此外,我们还发现,额下回(接近经典语言区)在估算时激活更大,这表明在估算时也有语言区域参与加工,这有可能是在任务比较阶段,儿童采用复述的策略来选择合适的答案、故语言区域有较大的激活。另外,前额叶的中部(MPPC)和两侧的额叶背外侧区域在估算时激活更大, 这两个脑区和认知加工(特别是和注意、执行加工、决策等相关的任务)的关系非常密切[9,10]。估算任务中,这些脑区的激活可能是由于任务的难度引起的,估算对普通儿童来说比精算要难得多,加工的过程更加复杂,需要调动更多的认知资源。
有一点需要特别注意,珠心算组和对照组在精算-估算的比较中,均未发现显著的激活。而在以往的成人精算、估算实验研究中,均发现左侧脑区,特别是语言区域,在精算时有更多的激活[1, 3]。造成结果不一致的原因可能有两个。一、数学认知加工能力有一个发展的过程,10岁左右的儿童,他们的精算、估算的脑机制还不成熟,所以在脑活动模式上和成人有差异。二、本研究中,没有直接的成人被试的结果作为对照,只是参照以往国外的研究结果,不排除有这样的可能:中国人精算、估算的脑机制和西方人有差异。唐一源等人就发现使用汉语的中国人和英美语系的西方人在数学认知加工的脑机制上是有差别的[16]。这方面需要进一步用实验来验证。
在精算和估算两种条件下,珠心算组比对照组激活强的区域主要集中在经典的默认活动网络内[11-15],实验结果和我们的假设一致,即在两种任务中,珠心算组儿童计算加工的效率更高,需要的资源更少,负激活的程度比对照组要低。估算时,对照组-珠心算组,激活的脑区主要集中在左侧语言区(额下回)、左右两侧脑岛、右侧额上回、前额叶的中部(MPFC)/辅助运动区(SMA)、左侧顶上小叶及小脑部分。语言区域的激活,表明与珠心算组相比较,对照组在估算时依赖语言加工的成分更多;右侧额上回、前额叶的中部(MPFC)/辅助运动区(SMA)的激活差异,在一定程度上可能反映了任务的难度,即完成估算任务对对照组来说相对要难一些,这在行为结果中也有所反应,估算任务中,对照组的准确率比珠心算组低,反应时相对也要长。两侧脑岛和小脑部分的激活差异,还有待于进一步的探讨。精算和估算时,对照组在顶叶都有较大的激活,这和我们的预期不一致,有可能反映了对照组有更多的脑区参与了精算、估算加工过程,有待于对数据做进一步分析。
5、小结
本研究应用fMRI技术检测珠心算儿童和普通儿童在一位数精算、估算时的脑活动情况,旨在考察两方面的内容:一、儿童和成人是否有相同的精算、估算神经机制;二、珠心算练习是否会影响儿童精算、估算的脑机制。从目前的研究结果来看,儿童精算、估算的脑机制和成人是有差别的,其原因可能是由于儿童的数字认知能力还不成熟。珠心算练习对儿童精算、估算加工,有两方面的影响。一、珠心算练习促进了儿童精算、估算的加工能力,完成相同的任务,所需要的资源比对照组更少,效率更高;二、珠心算儿童可能有相同的精算、估算神经机制。另外,对普通儿童来说,采用的计算策略不是单一的,特别是在估算任务中,语言表征和非语言的视觉空间表征可能都有参与。
本研究的不足之处:
一、实验任务的设置需要进一步调整,作为对照的基线任务应该选择任务难度与当前任务相当或者略微简单一点的任务。
二、数据分析还有待于进一步深入,精算、估算加工网络的联结情况更值得关注。
三、在理论水平上有待于提高,应该结合数字加工模型来对实验结果进行探讨。
四、本研究中,缺少成人被试的数据,对于考察儿童和成人是否有相同的精算、估算神经机制,还缺乏确凿的证据,需要在接下来的研究中予以验证。
参考文献
[1] Dehaene, S., Spelke, E., Pinel, P., Stanescu, R.,Tsivkin, S. (1999). Sources of mathematical thinking: behavioralbrain imaging evidence. Science 284, 970–974.
[2] Dehaene, S., Piazza, M., Pinel, P.,Cohen, L. (2003). Three parietal circuits for number processing. Cogn. Neuropsychol. 20, 487–506.
[3] Stanescu-Cosson, R., Pinel, P., van de Moortele, P.-F., Bihan, D. Le, Cohen, L, .and Dehaene, S. (2000).Understanding dissociations in dyscalculia: A brain imaging study of the impact of number size on the cerebral networks for exactapproximate calculation. Brain 123, 2240-2255
[4] Zago L, Pesenti M, Mellet E, Crivello F, Mazoyer B et al.( 2001). Neural correlates of simplecomplex mental calculation. Neuroimage.13, 314–327.
[5] Knops, A., Thirion, B., Hubbard, E. M., Michel, V.Dehaene, S.( 2009). Recruitment of an Area Involved in Eye Movements: During Mental Arithmetic. Science, 324, 1583-1585
[6] Rousselle, L.,Noel, M.-P. (2008). Mental Arithmetic in Children With Mathematics Learning Disabilities: The Adaptive Use of Approximate Calculation in an Addition Verification Task. J Learn Disabil 41, 498-513
[7] Jordan, N.C., Hanich, L.B., Kaplan, D. Arithmetic fact mastery in young children: A longitudinal investigation (2003). Journal of Experimental Child Psychology 85(2):103-119
[8] Kawashima, R., Taira, M., Okita, K., Inoue, K., Tajima ,N., et al. (2004).A functional MRI study of simple arithmetic--a comparison between childrenadults. Brain Res. Cogn Brain Res. 18(3):227-33
[9] Cohen, M.X., Heller, A.S., Ranganath, C. Functional connectivity with anterior cingulateorbitofrontal cortices during decision-making. (2005),Cognitive Brain Research 23 61– 70
[10] Hanakawaa,T., Honda, M., Okada, T., Fukuyama, H., Shibasaki, H. Differential activity in the premotor cortex subdivisions in humans during mental calculationverbal rehearsal tasks: a functional magnetic resonance imaging study. (2003). Neuroscience Letters. 347,199–201
[11] Greicius, M.D., Krasnow, B., Reiss, A.L., Menon, V., 2003. Functional connectivity in the resting brain: a network analysis of the default mode hypothesis. Proceedings of the National Academy of Sciences of the United States of America 100, 253-258.
[12] Greicius, M.D., Menon, V., 2004. Default-mode activity during a passive sensory task: Uncoupled from deactivation but impacting activation. J Cogn Neurosci 16, 1484-1492
[13] Raichle, M.E., Macleod, A.M., Abraham Z, S., William J, P., Gusnard, D.A., Shulman, G.L., 2001. A default mode of brain function. Proc Natl Acad Sci USA 98, 676-682.
[14] Raichle, M.E., Mintun, M.A., 2006. Brain workbrain imaging. Annual Review of Neuroscience 29, 449-476.
[15] Raichle, M.E., Snyder, A.Z., 2007. A default mode of brain function: a brief history of an evolving idea. Neuroimage 37, 1083-1090.
[16] Tang, Y., Zhang, W., Chen, K., Feng, S., Ji, Y., Shen, J., Reiman, E. M.,and Liu Y. (2006). Arithmetic processing in the brain shaped by cultures. PNAS 103, 10775-10780






